题目内容
(2012•鼓楼区一模)(1)6位新同学参加夏令营,大家彼此握手,互相介绍自己,这6位同学共握手多少次?小莉是这样思考的:每一位同学要与其他5位同学握手5次,6位同学握手5×6=30次,但每两位同学握手2次,因此这6位同学共握手
=15次.依此类推,12位同学彼此握手,共握手
(2)我们经常会遇到与上面类似的问题,如:2条直线相交,最多只有1个交点;3条直线相交,最多有3个交点;…;求20条直线相交,最多有多少个交点?
(3)在上述问题中,分别把人、线看成是研究对象,两人握手、两线相交是研究对象间的一种关系,要求的握手总次数、最多交点数就是求所有对象间的不同关系总数.它们都是满足一种相同的模型.请结合你学过的数学知识和生活经验,编制一个符合上述模型的问题.
(4)请运用解决上述问题的思想方法,探究n边形共有多少条对角线?写出你的探究过程及结果.
| 5×6 | 2 |
66
66
次.(2)我们经常会遇到与上面类似的问题,如:2条直线相交,最多只有1个交点;3条直线相交,最多有3个交点;…;求20条直线相交,最多有多少个交点?
(3)在上述问题中,分别把人、线看成是研究对象,两人握手、两线相交是研究对象间的一种关系,要求的握手总次数、最多交点数就是求所有对象间的不同关系总数.它们都是满足一种相同的模型.请结合你学过的数学知识和生活经验,编制一个符合上述模型的问题.
(4)请运用解决上述问题的思想方法,探究n边形共有多少条对角线?写出你的探究过程及结果.
分析:(1)根据总结的公式代入12即可求得结果;
(2)将握手问题推广至直线交点问题即可得到相同的运算公式;
(3)将以上问题推广至单循环比赛中即可得到答案;
(4)首先得到从一个顶点引出的对角线的条数然后乘以顶点个数除以2即可.
(2)将握手问题推广至直线交点问题即可得到相同的运算公式;
(3)将以上问题推广至单循环比赛中即可得到答案;
(4)首先得到从一个顶点引出的对角线的条数然后乘以顶点个数除以2即可.
解答:解:(1)
=66.…(1分)
(2)每一条直线最多与其它19条直线相交,20条直线交点20×19=380个,但每两条直线相交2次,因此这20条直线相交,最多有
=190个交点.…(4分)
(3)答案不唯一,如:现有12个乒乓球队参加乒乓球循环赛(每个队都要与其他队比赛1场),共需比赛多少场?…(7分)
(4)n边形每一个顶点与其它不相邻的(n-3)个顶点连成对角线,共有n(n-3)条对角线,但每两个不相邻的顶点相连2次,因此n边形共有
)(n>3)条对角线.…(10分)
| 12×11 |
| 2 |
(2)每一条直线最多与其它19条直线相交,20条直线交点20×19=380个,但每两条直线相交2次,因此这20条直线相交,最多有
| 20×19 |
| 2 |
(3)答案不唯一,如:现有12个乒乓球队参加乒乓球循环赛(每个队都要与其他队比赛1场),共需比赛多少场?…(7分)
(4)n边形每一个顶点与其它不相邻的(n-3)个顶点连成对角线,共有n(n-3)条对角线,但每两个不相邻的顶点相连2次,因此n边形共有
| n(n-3) |
| 2 |
点评:本题考查了规律型问题,可以将以上问题总结为握手问题,解题的关键是找到问题的通项公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
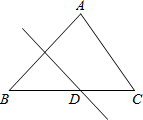 (2012•鼓楼区一模)如图,△ABC中,∠ABC=45°,AC=10,对折使点B与点A重合,折痕与BC交于点D,BD:DC=4:3,则DC的长为( )
(2012•鼓楼区一模)如图,△ABC中,∠ABC=45°,AC=10,对折使点B与点A重合,折痕与BC交于点D,BD:DC=4:3,则DC的长为( )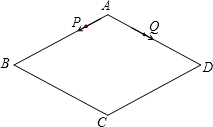 /s;点Q沿折线A-D-C-B运动,速度为1.5cm/s.当一点到达终点时,另一点也随即停止运动.若点P、Q同时从点A出发,运动时间为t s.
/s;点Q沿折线A-D-C-B运动,速度为1.5cm/s.当一点到达终点时,另一点也随即停止运动.若点P、Q同时从点A出发,运动时间为t s.