题目内容
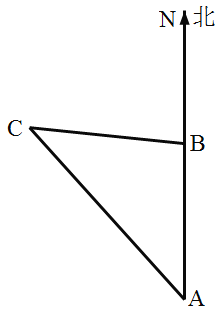
【题目】如图,![]() 是直角三角形,
是直角三角形,![]() ,
,![]() ,以点
,以点![]() 为旋转中心,将
为旋转中心,将![]() 旋转到
旋转到![]() 的位置,且使
的位置,且使![]() 经过点
经过点![]() .
.

![]() 求
求![]() 的度数,判断
的度数,判断![]() 的形状;
的形状;
![]() 求线段
求线段![]() 与线段
与线段![]() 的数量关系.
的数量关系.
【答案】![]() ∠ACA′=60°,
∠ACA′=60°,![]() 是等边三角形;
是等边三角形;![]() .
.
【解析】
(1)证明∠BAC=60°;证明AC=A′C,得到∠A′=∠A′AC=60°,求出∠ACA′=60°;
(2)由△ABC≌△A′B′C′得到∠A′CB=∠ACB=90°,求得∠B′=∠B=30°,由(1)知:∠ACA′=60°,得到AC=AB′,于是得到结论.
(1)∵∠ACB=90°,∠B=30°,∴AB=2AC,∠BAC=60°;
∵△ABC≌△A′B′C′,∴∠A′=∠BAC=60°,AC=A′C,∴∠A′=∠A′AC=60°,∴∠ACA′=180°﹣120°=60°,∴△ACA′是等边三角形;
(2)∵△ABC≌△A′B′C′,∴∠A′CB=∠ACB=90°,∠B′=∠B=30°,A′B′=AB,由(1)知:∠ACA′=60°,∴∠ACB′=30°,∴AC=AB′,∴AB=A′B′=AA′+AB′=2AC=2AC.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目