Question

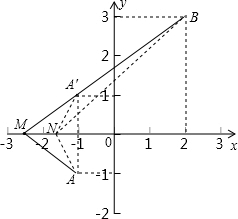
如图，在直角坐标系内有两个点A（-1，-1），B（2，3），若M为x轴上一点，且使MB-MA最大，求M点的坐标，并说明理由．

Answer 1

作点A关于x轴的对称点A'，
作直线BA'交x轴于点M，
由对称性知MA'=MA，MB-MA=MB-MA'=A'B，
若N是x轴上异于M的点，
则NA'=NA，这时NB-NA=NB-NA'＜A'B=MB-MA，
所以，点M就是使MB-MA的最大的点，MB-MA的最大值为A'B，
设直线A'B的解析式为y=kx+b，
则

1=-k+b 3=2k+b

解得k=

2

3

，b=

5

3

，即直线A'B的解析式为y=

2

3

x+

5

3

，
令y=0，得x=-

5

2

，故M点的坐标为（-

5

2

，0）．
故答案为：（-

5

2

，0）．