题目内容
如图,在正方形网格中,每个小正方形的边长都为1
(1)如图1,两个半径为1的圆相交,则阴影部分的面积为
π-1
π-1;
(2)图2是以(1)中的图形为基本图形,通过一组图形变换得到的,这组变换可以是
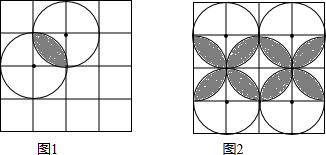
(1)如图1,两个半径为1的圆相交,则阴影部分的面积为
| 1 |
| 2 |
| 1 |
| 2 |
(2)图2是以(1)中的图形为基本图形,通过一组图形变换得到的,这组变换可以是
①②
①②
.(写出一组即可)(填入序号).①轴对称变换;②平移变换;③旋转变换.
分析:(1)先求出正方形ABCD的面积,然后求出扇形ABC的面积,利用面积阴影部分的面积=1-2(S□ABCD-S扇形ABC)即可求出;
(2)结合两个图形的形状,及轴对称变换、平移变换和旋转变换性质即可解答.
(2)结合两个图形的形状,及轴对称变换、平移变换和旋转变换性质即可解答.
解答:解:(1)S□ABCD=1×1=1,
S扇形ABC=
×π×12=
.
∴阴影部分的面积=1-2(S□ABCD-S扇形ABC)=
π-1;
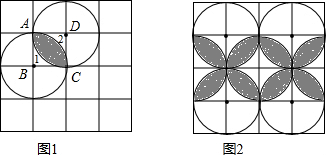
(2)图2中的图形可以通过①轴对称变换和②平移变换得到.
故答案为:
π-1;①②.
S扇形ABC=
| 90 |
| 360 |
| π |
| 4 |
∴阴影部分的面积=1-2(S□ABCD-S扇形ABC)=
| 1 |
| 2 |

(2)图2中的图形可以通过①轴对称变换和②平移变换得到.
故答案为:
| 1 |
| 2 |
点评:本题考查几何变换的类型,难度适中,解答这类问题可以动手操作一下,同时也考查了学生的想象能力.

练习册系列答案
相关题目
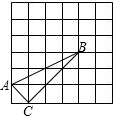 如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )
如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
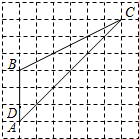 如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE=
如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE= 6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
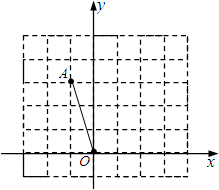 如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).
如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).