题目内容
若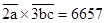 ,其中a,b,c代表非零数字,则
,其中a,b,c代表非零数字,则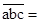 ;
;
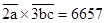 ,其中a,b,c代表非零数字,则
,其中a,b,c代表非零数字,则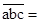 ;
;117
考点:数的十进制.
分析:首先根据题意得:(20+a)(300+10b+c)=117,又由百位数字是6,a,b,c代表非零数字,可得2a+3b≤6,即可求得a与b的值,代入易得c的值,则问题得解.
解答:解:∵
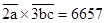
∴(20+a)(300+10b+c)=6000+200b+20c+300a+10ab+ac=6000+100(2a+3b)+20c+10ab+ac,
∵百位数字是6,a,b,c代表非零数字,
∴2a+3b≤6,
∴a=1,b=1,
∵(20+a)(300+10b+c)=6000+500+20c+10+c=6657,
∴c=7.
故
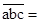 =117.
=117.故答案为:117.

练习册系列答案
相关题目
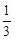 。此时,又增加6个人,那么要完成剩余的工程,还需要
。此时,又增加6个人,那么要完成剩余的工程,还需要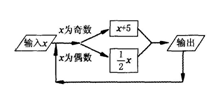
 .
.