题目内容
【题目】如图,二次函数的![]() 的图象经过点
的图象经过点![]() 、
、![]() .
.
(![]() )求二次函数
)求二次函数![]() 的关系式.
的关系式.
(![]() )把
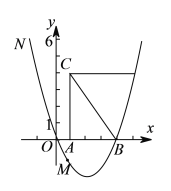
)把![]() 放在坐标系内,其中
放在坐标系内,其中![]() ,点
,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,![]() ,将
,将![]() 沿
沿![]() 轴向右平移,当点
轴向右平移,当点![]() 落在抛物线上时,求
落在抛物线上时,求![]() 平移的距离.
平移的距离.
【答案】(1) ![]() ;(2)
;(2)![]() 平移的距离为
平移的距离为![]() .
.
【解析】
(1)将M、N两点坐标代入抛物线解析式,得到关于b、c的方程组,解方程组求出b、c即可;(2)先在![]() 中求出AC的长为4,得
中求出AC的长为4,得![]() 点坐标为
点坐标为![]() 或
或![]() ,再设平移后的
,再设平移后的![]() 点坐标为
点坐标为![]() 或
或![]() ,然后依次将C点坐标代入求解,并及时注意检验取舍,最后让C点的横坐标减去OA的长即为平移的距离.
,然后依次将C点坐标代入求解,并及时注意检验取舍,最后让C点的横坐标减去OA的长即为平移的距离.
(![]() )根据题意,得
)根据题意,得
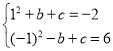 ,
,
解得![]() ,
,
∴二次函数![]() 的关系为
的关系为![]() .
.
(![]() )∵
)∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() 点坐标为
点坐标为![]() 或
或![]() ,
,
设平移后的![]() 点坐标为
点坐标为![]() 或
或![]() ,
,
∵![]() 沿
沿![]() 轴向右平移,
轴向右平移,
∴![]() ,
,
将![]() 代入二次函数解析式中,得
代入二次函数解析式中,得
![]() ,
,
解得![]() ,
,![]() (舍),
(舍),
将![]() 代入二次函数解析式中,得
代入二次函数解析式中,得
![]() ,
,
方程无解,
![]() 平移的距离为
平移的距离为![]() .
.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
【题目】如图,在△ABC中,∠ABC=90°,∠CAB=30°,AB=4.5cm.D是线段AB上的一个动点,连接CD,过点D作CD的垂线交CA于点E.设AD=xcm,CE=ycm.(当点D与点A或点B重合时,y的值为5.2)
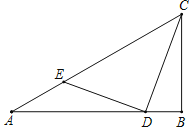
探究函数y随自变量x的变化而变化的规律.
(1)通过取点、画图、测量,得到了x与y的几组对应值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 |
y/cm | 5.2 | 4.8 | 4.4 | 4.0 | 3.8 | 3.6 | 3.5 | 3.6 | 5.2 |
(要求:补全表格,相关数值保留一位小数)
(2)建立平面直角坐标系xOy,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当CE=2AD时,AD的长度约为 cm(结果保留一位小数).