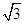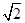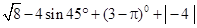题目内容
Rt△ABC中,∠A=900,BC=4,有一个内角为600,点P是直线AB上不同于A、B的一点,且∠ACP=300,则PB的长为 .
4或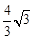 或
或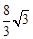 。
。
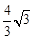 或
或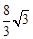 。
。分两种情况考虑:
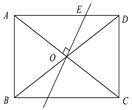
当∠ABC=60°时,如图所示:
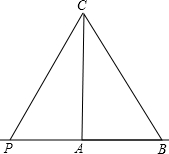
∵∠CAB=90°,∴∠BCA=30°。
又∵∠PCA=30°,∴∠PCB=∠PCA+∠ACB=60°。
又∵∠ABC=60°,∴△PCB为等边三角形。
又∵BC=4,∴PB=4。
当∠ABC=30°时,
(i)当P在A的右边时,如图所示:

∵∠PCA=30°,∠ACB=60°,∴∠PCB=90°。
又∠B=30°,BC=4,
∴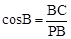 ,即
,即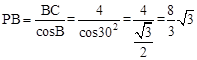 。
。
(ii)当P在A的左边时,如图所示:
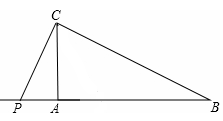
∵∠PCA=30°,∠ACB=60°,∴∠BCP=30°。
又∠B=30°,∴∠BCP=∠B。∴CP=BP。
在Rt△ABC中,∠B=30°,BC=4,∴AC=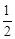 BC=2。
BC=2。
根据勾股定理得: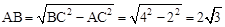 ,
,
∴AP=AB-PB=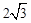 -PB。
-PB。
在Rt△APC中,根据勾股定理得:AC2+AP2=CP2=BP2,即22+(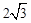 -PB)2=BP2,
-PB)2=BP2,
解得:BP=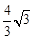 。
。
综上所述,BP的长为4或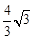 或
或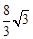 。
。
当∠ABC=60°时,如图所示:

∵∠CAB=90°,∴∠BCA=30°。
又∵∠PCA=30°,∴∠PCB=∠PCA+∠ACB=60°。
又∵∠ABC=60°,∴△PCB为等边三角形。
又∵BC=4,∴PB=4。
当∠ABC=30°时,
(i)当P在A的右边时,如图所示:

∵∠PCA=30°,∠ACB=60°,∴∠PCB=90°。
又∠B=30°,BC=4,
∴
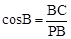 ,即
,即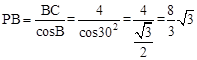 。
。(ii)当P在A的左边时,如图所示:

∵∠PCA=30°,∠ACB=60°,∴∠BCP=30°。
又∠B=30°,∴∠BCP=∠B。∴CP=BP。
在Rt△ABC中,∠B=30°,BC=4,∴AC=
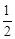 BC=2。
BC=2。根据勾股定理得:
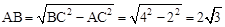 ,
,∴AP=AB-PB=
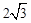 -PB。
-PB。在Rt△APC中,根据勾股定理得:AC2+AP2=CP2=BP2,即22+(
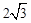 -PB)2=BP2,
-PB)2=BP2,解得:BP=
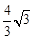 。
。综上所述,BP的长为4或
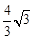 或
或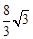 。
。
练习册系列答案
相关题目

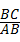 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题: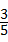 ,其中∠A为锐角,试求sadA的值.
,其中∠A为锐角,试求sadA的值.
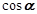 的值是( )
的值是( )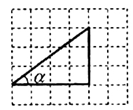
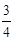
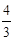
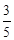
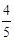
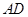 ∥
∥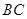 ,坝高10m,迎水坡面
,坝高10m,迎水坡面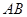 的坡度
的坡度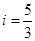 ,审核组专家看后,从力学的角度对此方案提出了建议,李设计师决定在原方案的基础上,将迎水坡面
,审核组专家看后,从力学的角度对此方案提出了建议,李设计师决定在原方案的基础上,将迎水坡面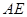 的坡度
的坡度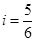 .
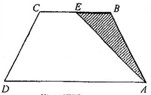
.
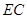 方向拓宽
方向拓宽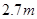 ,求坝底将会沿
,求坝底将会沿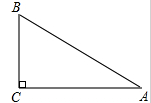
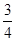
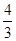
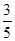
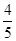
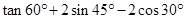 的结果是( )
的结果是( )