题目内容
已知等腰梯形上、下底之差等于一腰长，则相邻两个角为
- A.30°，150°
- B.45°，135°
- C.60°，120°
- D.75°，105°
C
分析：过点D作DE∥AB，因为上、下底之差等于一腰长，所以DEC是等边三角形，从而得到∠ABE=60°∠BAD=120°．
解答：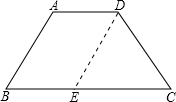
解：过点D作DE∥AB，则AD=BE，EC就是两底的差，差等于一腰长，则△DEC是等边三角形，因而∠C=60°，根据AD∥BC，得到∠ADC=180-60=120°，即相邻两个角为60°，120度．相邻两个角为60°，120度．故选C
点评：此题考查等腰梯形的性质及梯形中常见的辅助线的作法．
分析：过点D作DE∥AB，因为上、下底之差等于一腰长，所以DEC是等边三角形，从而得到∠ABE=60°∠BAD=120°．
解答：
解：过点D作DE∥AB，则AD=BE，EC就是两底的差，差等于一腰长，则△DEC是等边三角形，因而∠C=60°，根据AD∥BC，得到∠ADC=180-60=120°，即相邻两个角为60°，120度．相邻两个角为60°，120度．故选C点评：此题考查等腰梯形的性质及梯形中常见的辅助线的作法．
练习册系列答案
相关题目
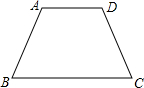如图所示，已知等腰梯形ABCD中，AD∥BC，下底BC与上底AD的差恰好等于腰长AB，则∠BAD=（ ）