题目内容
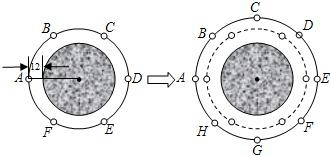
如图所示,中心阴影部分为一圆形餐桌,开始时有A、B、C、D、E、F共6人围成圆形绕桌而坐.已知餐桌所在圆的半径为60厘米,每人距餐桌外缘的最短距离均为12厘米,相邻2人间的弧长均相等.席间又有G、H 2人加入,于是每人都将座位向外移了移,并保持8人仍围成圆形绕桌而坐,且相邻2人间的弧长与6人就餐时相等(不考虑其它因素).(1)问:相邻2人间的弧长是多少?(结果保留π)
(2)求8人就餐时其中任意一人距餐桌外缘的最短距离是多少?
分析:(1)先求得相邻2人间的弧所对的圆心角的度数,再按弧长公式计算即可;
(2)设8人就餐时其中任意一人距餐桌外缘的最短距离是x厘米.根据题意列出等式,即可求得答案.
(2)设8人就餐时其中任意一人距餐桌外缘的最短距离是x厘米.根据题意列出等式,即可求得答案.
解答:解:(1)
=24π.
即相邻2人间的弧长是24π厘米.(3分)
(2)设8人就餐时其中任意一人距餐桌外缘的最短距离是x厘米.
依题意,得
=24π.(6分)
解之得x=36.
∴8人就餐时其中任意一人距餐桌外缘的最短距离是36厘米.(9分).
| 2π(12+60) |
| 6 |
即相邻2人间的弧长是24π厘米.(3分)
(2)设8人就餐时其中任意一人距餐桌外缘的最短距离是x厘米.
依题意,得
| 2π(x+60) |
| 8 |
解之得x=36.
∴8人就餐时其中任意一人距餐桌外缘的最短距离是36厘米.(9分).
点评:本题考查了弧长的计算以及一元一次方程的应用,是一道综合题,难度偏大.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
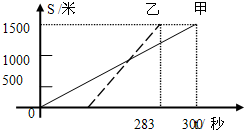 7、如图,甲乙两人在一次赛跑中,路程s和t时间的关系如图所示(实线部分为甲,虚线部分为乙)李丽同学得到如下信息,其中错误的是( )
7、如图,甲乙两人在一次赛跑中,路程s和t时间的关系如图所示(实线部分为甲,虚线部分为乙)李丽同学得到如下信息,其中错误的是( )
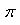 )
)