题目内容
如图,二次函数图象的顶点为坐标原点O,y轴为对称轴,且经过点A(3,3),一次函数的图 象经过点A和点B(6,0).
象经过点A和点B(6,0).
(1)求二次函数与一次函数的解析式;
(2)如果一次函数图象与y轴相交于点C,E是抛物线上OA段上一点,过点E作y轴平行的直线DE与直线AC交于点D,∠DOE=∠EDA,求点E的坐标;
(3)点M是线段AC延长线上的一个动点,过点M作y轴的平行线交抛物线于F,以点O、C、M、F为顶点的四边形能否为菱形?若能,求出点F的坐标;若不能,请说明理由.
解: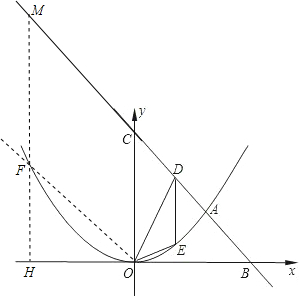 (1)设二次函数的解析式为y=ax2,
(1)设二次函数的解析式为y=ax2,
把点A(3,3)代入得3=a×32,解得a= ;
;
设一次函数的解析式为y=kx+b,
把点A(3,3)、点B(6,0)代入得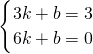 ,解得
,解得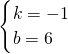 ,
,
所以二次函数与一次函数的解析式分别为y= x2,y=-x+6;
x2,y=-x+6;
(2)C点坐标为(0,6),
∵DE∥y轴,
∴∠ODE=∠COD,∠EDA=∠OCD,
∵∠DOE=∠EDA,
∴∠DOE=∠OCD,
∴△OCD∽△DOE,
∴OC:OD=OD:DE,即OD2=OC•DE,
设E点坐标为(a, a2),则D点坐标为(a,6-a),
a2),则D点坐标为(a,6-a),
OD2=a2+(6-a)2,=2a2-12a+36,OC=6,DE=6-a- a2,
a2,
∴2a2-12a+36=6(6-a- a2),解得a1=0,a2=
a2),解得a1=0,a2= ,
,
∵E是抛物线上OA段上一点,
∴0<a<3,
∴a= ,
,
∴点E坐标为( ,
, );
);
(3)以点O、C、M、F为顶点的四边形不能为菱形.理由如下:
如图,过O点作OF∥AC交抛物线于F,过F点作FM∥y轴交AC延长线于M点,交x轴于H点,
则四边形OCMF为平行四边形,
∵OC=OB=6,
∴△OCB为等腰直角三角形,
∴∠OBC=45°,
∴∠HOF=45°,
∴△OHF为等腰直角三角形,
∴HO=HF,
设F点坐标为(m,-m)(m>0),
把F(m,-m)代入y= x2得-m=
x2得-m= m2,解得m1=0,m2=-3,
m2,解得m1=0,m2=-3,
∴m=-3,
∴HO=HF=3,
∴OF= OH=3
OH=3 ,
,
而OC=6,
∴四边形OCMF不为菱形.
分析:(1)利用待定系数法求二次函数与一次函数的解析式;
(2)由于DE∥y轴,根据平行线的性质得∠ODE=∠COD,∠EDA=∠OCD,而∠DOE=∠EDA,则∠DOE=∠OCD,根据相似三角形的判定方法得到△OCD∽△DOE,所以OC:OD=OD:DE,即OD2=OC•DE,
设E点坐标为(a, a2),则D点坐标为(a,6-a),利用勾股定理计算出OD2=a2+(6-a)2,=2a2-12a+36,而OC=6,DE=6-a-
a2),则D点坐标为(a,6-a),利用勾股定理计算出OD2=a2+(6-a)2,=2a2-12a+36,而OC=6,DE=6-a- a2,则2a2-12a+36=6(6-a-
a2,则2a2-12a+36=6(6-a- a2),解得a=
a2),解得a= ,即可确定E点坐标;
,即可确定E点坐标;
(3)过O点作OF∥AC交抛物线于F,过F点作FM∥y轴交AC延长线于M点,交x轴于H点,则四边形OCMF为平行四边形,易得∠OBC=45°,则∠HOF=45°,于是△OHF为等腰直角三角形,得到HO=HF,
设F点坐标为(m,-m)(m>0),把F点坐标代入二次函数解析式可求出m=-3,得到HO=HF=3,OF= OH=3
OH=3 ,而OC=6,所以判断四边形OCMF不为菱形.
,而OC=6,所以判断四边形OCMF不为菱形.
点评:本题考查了二次函数综合题:会待定系数法求二次函数与一次函数的解析式;掌握等腰直角三角形的性质和菱形的判定方法;在几何计算中常利用三角形相似比和勾股定理.
 (1)设二次函数的解析式为y=ax2,
(1)设二次函数的解析式为y=ax2,把点A(3,3)代入得3=a×32,解得a=
 ;
;设一次函数的解析式为y=kx+b,
把点A(3,3)、点B(6,0)代入得
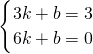 ,解得
,解得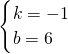 ,
,所以二次函数与一次函数的解析式分别为y=
 x2,y=-x+6;
x2,y=-x+6;(2)C点坐标为(0,6),
∵DE∥y轴,
∴∠ODE=∠COD,∠EDA=∠OCD,
∵∠DOE=∠EDA,
∴∠DOE=∠OCD,
∴△OCD∽△DOE,
∴OC:OD=OD:DE,即OD2=OC•DE,
设E点坐标为(a,
 a2),则D点坐标为(a,6-a),
a2),则D点坐标为(a,6-a),OD2=a2+(6-a)2,=2a2-12a+36,OC=6,DE=6-a-
 a2,
a2,∴2a2-12a+36=6(6-a-
 a2),解得a1=0,a2=
a2),解得a1=0,a2= ,
,∵E是抛物线上OA段上一点,
∴0<a<3,
∴a=
 ,
,∴点E坐标为(
 ,
, );
);(3)以点O、C、M、F为顶点的四边形不能为菱形.理由如下:
如图,过O点作OF∥AC交抛物线于F,过F点作FM∥y轴交AC延长线于M点,交x轴于H点,
则四边形OCMF为平行四边形,
∵OC=OB=6,
∴△OCB为等腰直角三角形,
∴∠OBC=45°,
∴∠HOF=45°,
∴△OHF为等腰直角三角形,
∴HO=HF,
设F点坐标为(m,-m)(m>0),
把F(m,-m)代入y=
 x2得-m=
x2得-m= m2,解得m1=0,m2=-3,
m2,解得m1=0,m2=-3,∴m=-3,
∴HO=HF=3,
∴OF=
 OH=3
OH=3 ,
,而OC=6,
∴四边形OCMF不为菱形.
分析:(1)利用待定系数法求二次函数与一次函数的解析式;
(2)由于DE∥y轴,根据平行线的性质得∠ODE=∠COD,∠EDA=∠OCD,而∠DOE=∠EDA,则∠DOE=∠OCD,根据相似三角形的判定方法得到△OCD∽△DOE,所以OC:OD=OD:DE,即OD2=OC•DE,
设E点坐标为(a,
 a2),则D点坐标为(a,6-a),利用勾股定理计算出OD2=a2+(6-a)2,=2a2-12a+36,而OC=6,DE=6-a-
a2),则D点坐标为(a,6-a),利用勾股定理计算出OD2=a2+(6-a)2,=2a2-12a+36,而OC=6,DE=6-a- a2,则2a2-12a+36=6(6-a-
a2,则2a2-12a+36=6(6-a- a2),解得a=
a2),解得a= ,即可确定E点坐标;
,即可确定E点坐标;(3)过O点作OF∥AC交抛物线于F,过F点作FM∥y轴交AC延长线于M点,交x轴于H点,则四边形OCMF为平行四边形,易得∠OBC=45°,则∠HOF=45°,于是△OHF为等腰直角三角形,得到HO=HF,
设F点坐标为(m,-m)(m>0),把F点坐标代入二次函数解析式可求出m=-3,得到HO=HF=3,OF=
 OH=3
OH=3 ,而OC=6,所以判断四边形OCMF不为菱形.
,而OC=6,所以判断四边形OCMF不为菱形.点评:本题考查了二次函数综合题:会待定系数法求二次函数与一次函数的解析式;掌握等腰直角三角形的性质和菱形的判定方法;在几何计算中常利用三角形相似比和勾股定理.

练习册系列答案
相关题目
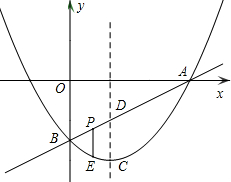 段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.
段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.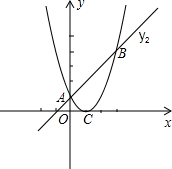 如图,二次函数
如图,二次函数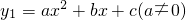 的图象与一次函数y2=x+b的图象交于A(0,1),B两点.C(1,0)为二次函数图象的顶点.
的图象与一次函数y2=x+b的图象交于A(0,1),B两点.C(1,0)为二次函数图象的顶点.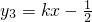 (k>0)与函数f的图象只有两个交点时,求k的值.
(k>0)与函数f的图象只有两个交点时,求k的值.


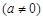 图象的顶点为
图象的顶点为 ,与
,与 轴交于
轴交于 、
、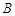 两点(
两点( :
: 对称.
对称.
 在直线
在直线 作直线
作直线 ∥
∥ 交直线
交直线 于
于 点,
点, 、
、 分别为直线
分别为直线 、
、 、
、 ,求
,求 和的最小值.
和的最小值.