题目内容
如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若A点的坐标为(-1,0),则点C的坐标为 .


分析:先连接OE,由于正六边形是轴对称图形,并设EF交Y轴于G,那么∠GOE=30°;在Rt△GOE中,则GE=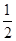 ,OG=
,OG= 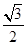 .即可求得E的坐标,和E关于Y轴对称的F点的坐标,其他坐标类似可求出.
.即可求得E的坐标,和E关于Y轴对称的F点的坐标,其他坐标类似可求出.
解:连接OE,由正六边形是轴对称图形知:
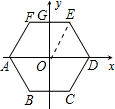
在Rt△OEG中,∠GOE=30°,OE=1.
∴GE=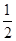 ,OG=
,OG=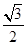 ∴A(-1,0),B(-
∴A(-1,0),B(-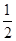 ,-
,-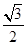 ),C(
),C(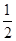 ,-
,-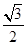 )D(1,0),E(
)D(1,0),E(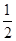 ,
,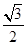 ),F(-
),F(-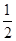 ,
,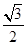 ).
).
故答案为:(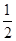 ,-
,-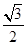 )
)
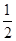 ,OG=
,OG= 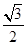 .即可求得E的坐标,和E关于Y轴对称的F点的坐标,其他坐标类似可求出.
.即可求得E的坐标,和E关于Y轴对称的F点的坐标,其他坐标类似可求出.解:连接OE,由正六边形是轴对称图形知:

在Rt△OEG中,∠GOE=30°,OE=1.
∴GE=
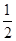 ,OG=
,OG=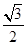 ∴A(-1,0),B(-
∴A(-1,0),B(-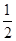 ,-
,-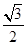 ),C(
),C(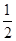 ,-
,-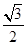 )D(1,0),E(
)D(1,0),E(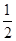 ,
,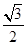 ),F(-
),F(-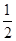 ,
,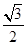 ).
).故答案为:(
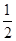 ,-
,-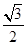 )
)
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目


 AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是 .
AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是 .
 心O,则折痕AB的长为( )
心O,则折痕AB的长为( )
 cm
cm