题目内容
【题目】[问题提出]
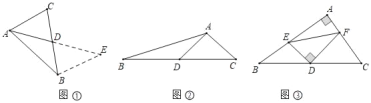
如图①,在△ABC中,若AB=6,AC=4,求BC边上的中线AD的取值范围.
[问题解决]
解决此问题可以用如下方法,延长AD到点E使DE=AD,再连结BE(或将△ACD绕着点D逆时针装转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形三边的关系即可判断,由此得出中线AD的取值范围是
[应用]
如图②,如图,在△ABC中,D为边BC的中点,已知AB=5,AC=3,AD=2.求BC的长
[拓展]
如图③,在△ABC中,∠A=90°,点D是边BC的中点,点E在边AB上,过点D作DF⊥DE交边AC于点F,连结EF,已知BE=4,CF=5,则EF的长为
【答案】(1)1<AD<5;(2)2![]() ;(3)
;(3)![]() .
.
【解析】
![]() 证明
证明![]() ≌
≌![]() 得
得![]() ,再根据三角形三边关系求得AE的取值范围,进而得结论;
,再根据三角形三边关系求得AE的取值范围,进而得结论;![]() 延长AD到E,使得
延长AD到E,使得![]() ,连接BE,证明
,连接BE,证明![]() ≌
≌![]() 得
得![]() ,再证明
,再证明![]() ,由勾股定理求得BD,进而得BC;
,由勾股定理求得BD,进而得BC;![]() 延长FD到G,使得
延长FD到G,使得![]() ,连接BG,EG,证明
,连接BG,EG,证明![]() ≌
≌![]() ,得
,得![]() ,
,![]() ,再证明
,再证明![]() ,由勾股定理求得EG,由线段垂直平分线性质得EF.
,由勾股定理求得EG,由线段垂直平分线性质得EF.
解:![]() 在
在![]() 和
和![]() 中,
中,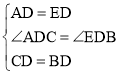 ,
,![]() ≌
≌![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故答案为![]() ;
;![]() 延长AD到E,使得
延长AD到E,使得![]() ,连接BE,如图
,连接BE,如图![]() ,
,
在![]() 和
和![]() 中,
中, ≌
≌![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() 延长FD到G,使得
延长FD到G,使得![]() ,连接BG,EG,如图
,连接BG,EG,如图![]() ,
,
在![]() 和
和![]() 中,
中, ,
,![]() ≌
≌![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目