题目内容
如图,在直角梯形OABC中,OA∥BC,∠B=90°,OA=6,AB=4,BC=3,以O为原点,以OA所在的直线为x轴建立平面直角坐标系,动点P从原点O出发,沿O?C?B?A的方向以每秒2两个单位长的速度运动,动点Q也从原点出发,在线段OA上以每秒1个单位长的速度向点A运动,点P、Q同时出发,当点Q运动到点A时,点P随之停止运动,设运动的时间为t(秒)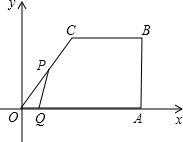 .
.(1)求点C的坐标和线段OC的长;
(2)设△OPQ的面积为S,求S与t之间的函数关系式;
(3)当点P在线段CB上运动时,是否存在以C、P、Q三点为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(1)要求线段OC的长和点C的坐标,只要从C作CD⊥OA交OA于D,利用正方形的性质就可读出点C的坐标及求出CD,OD长,然后利用勾股定理求OC的长.
(2)设△OPQ的面积为S,求S与t之间的函数关系式;就要利用三角形的面积公式计算.要计算三角形的面积就又要利用速度公式计算出三角形的底和高,然后利用面积公式计算.注意计算面积时,要根据点P的位置,分情况而计算.
(3)不存在,因为当点P运动在CB上时,CQ≥4,PQ≥4,CP≤3,要证明可先设一假设,证明假设不成立.
(2)设△OPQ的面积为S,求S与t之间的函数关系式;就要利用三角形的面积公式计算.要计算三角形的面积就又要利用速度公式计算出三角形的底和高,然后利用面积公式计算.注意计算面积时,要根据点P的位置,分情况而计算.
(3)不存在,因为当点P运动在CB上时,CQ≥4,PQ≥4,CP≤3,要证明可先设一假设,证明假设不成立.
解答: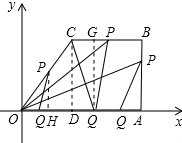 解:(1)过C作CD⊥OA交OA于D,
解:(1)过C作CD⊥OA交OA于D,
∵CD=AB=4,AD=BC=3,
∴OD=OA-AD=3,(2分)
∴点C的坐标为(3,4)(1分),
在Rt△OCD中,由勾股定理得OC=5.(1分)
(2)①当点P在OC上,即0≤t≤
时,
过P作PH⊥OA于点H,则PH∥CD,
∴△OPH∽△OCD,
∴
=
,即
=
,
∴PH=
,
∴S=
OQ•PH=
•t•
=
t2(2分);
②当点P在CB上,即
≤t≤4时,
∴S=
OQ•CD=
•t×4=2t.(2分)
③当点P在BA上,即4≤t≤6时,
∴S=
OQ•AP=
•t•(12-2t)=-t2+6t.(2分)
(3)不存在(1分)
当点P运动在CB上时,CQ≥4,PQ≥4,CP≤3,
假设CB上存在点P使△CPQ为等腰三角形,则CQ=PQ,
过Q作QG⊥BC交BC于G,则CG=PG=DQ,
∴2t-5=2(t-3),
∴-5=-6,不成立,
∴假设不成立,
∴当P点运动在线段CB上时,不存在以C,P,Q,
三点为顶点的三角形是等腰三角形.(3分)
 解:(1)过C作CD⊥OA交OA于D,
解:(1)过C作CD⊥OA交OA于D,∵CD=AB=4,AD=BC=3,
∴OD=OA-AD=3,(2分)
∴点C的坐标为(3,4)(1分),
在Rt△OCD中,由勾股定理得OC=5.(1分)
(2)①当点P在OC上,即0≤t≤
| 5 |
| 2 |
过P作PH⊥OA于点H,则PH∥CD,
∴△OPH∽△OCD,
∴
| PH |
| CD |
| OP |
| OC |
| PH |
| 4 |
| 2t |
| 5 |
∴PH=
| 8t |
| 5 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 8t |
| 5 |
| 4 |
| 5 |
②当点P在CB上,即
| 5 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
③当点P在BA上,即4≤t≤6时,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
(3)不存在(1分)
当点P运动在CB上时,CQ≥4,PQ≥4,CP≤3,
假设CB上存在点P使△CPQ为等腰三角形,则CQ=PQ,
过Q作QG⊥BC交BC于G,则CG=PG=DQ,
∴2t-5=2(t-3),
∴-5=-6,不成立,
∴假设不成立,
∴当P点运动在线段CB上时,不存在以C,P,Q,
三点为顶点的三角形是等腰三角形.(3分)
点评:本题综合考查了正方形,梯形和直角坐标系以及二次函数的综合应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 动时间为t(单位:秒).
动时间为t(单位:秒). (10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
(10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
 单位,移动时间记为t秒.
单位,移动时间记为t秒. 如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.
如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.