题目内容
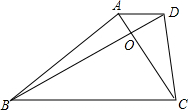 如图梯形ABCD中,AD∥BC,AC⊥BD,AC=5cm,BD=7cm,则此梯形中位线长为
如图梯形ABCD中,AD∥BC,AC⊥BD,AC=5cm,BD=7cm,则此梯形中位线长为分析:(1)根据题意过D作DE∥AC,交BC的延长线于E,则四边形ACED是平行四边形,得出AD=CE,DE=AC,再根据AC⊥BD判断出△BDE是直角三角形,最后根据勾股定理求解;
(2)根据题意过D作DF⊥BE,交BE于F,根据BD×DE=DF×BE求解.
(2)根据题意过D作DF⊥BE,交BE于F,根据BD×DE=DF×BE求解.
解答: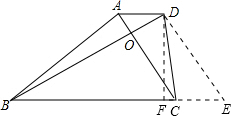 解:①如图所示,过D作DE∥AC,交BC的延长线于E,则四边形ACED是平行四边形,
解:①如图所示,过D作DE∥AC,交BC的延长线于E,则四边形ACED是平行四边形,
又∵AC⊥BD,
∴BD⊥DE,AD=CE,DE=AC,
在Rt△BDE中BE=
=
,
∵BE=AD+BC,
∴梯形中位线长为
cm;
②如图所示,过D作DF⊥BE,交BE于F,
在Rt△BDE中BD×DE=DF×BE,
∴DF=
,
∴梯形的面积=
×
=
cm2.
 解:①如图所示,过D作DE∥AC,交BC的延长线于E,则四边形ACED是平行四边形,
解:①如图所示,过D作DE∥AC,交BC的延长线于E,则四边形ACED是平行四边形,又∵AC⊥BD,
∴BD⊥DE,AD=CE,DE=AC,
在Rt△BDE中BE=
| 52+72 |
| 74 |
∵BE=AD+BC,
∴梯形中位线长为
| ||
| 2 |
②如图所示,过D作DF⊥BE,交BE于F,
在Rt△BDE中BD×DE=DF×BE,
∴DF=
| 35 | ||
|
∴梯形的面积=
| ||
| 2 |
| 35 | ||
|
| 35 |
| 2 |
点评:本题主要考查了梯形中位线定理,关键是根据题意添加常用的辅助线,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图梯形ABCD中,AD∥BC,AB=DC=2,∠ABC=60°,且BD⊥AC,EF是梯形的中位线,求EF的长.
如图梯形ABCD中,AD∥BC,AB=DC=2,∠ABC=60°,且BD⊥AC,EF是梯形的中位线,求EF的长.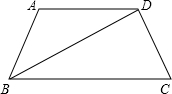 如图梯形ABCD中,AD∥BC,AB=AD=CD,BD⊥CD,求∠C的度数.
如图梯形ABCD中,AD∥BC,AB=AD=CD,BD⊥CD,求∠C的度数. 20、如图梯形ABCD中,∠B=60°,AB=5cm,将AB向右平移到点D,交BC于E,那么DE=
20、如图梯形ABCD中,∠B=60°,AB=5cm,将AB向右平移到点D,交BC于E,那么DE=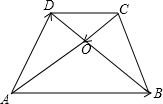
 15、如图梯形ABCD中,AD∥BC,AE∥DC,AD=5cm,梯形ABCD的周长为60cm,则△ABE的周长为( )
15、如图梯形ABCD中,AD∥BC,AE∥DC,AD=5cm,梯形ABCD的周长为60cm,则△ABE的周长为( )