题目内容
 如图,⊙O的半径是5,P是⊙O外一点,PO=8,∠OPA=30°,求AB和PB的长.
如图,⊙O的半径是5,P是⊙O外一点,PO=8,∠OPA=30°,求AB和PB的长.
分析:延长PO交⊙O于点C,过点O作OE⊥AB于E,∠OPA=30°,PO=8,可得OE=4;在Rt△OBE中,OB为半径,可以得出BE的长度,即可得到AB;再根据割线定理,有PD•PC=PB•PA,即可得出PB.
解答: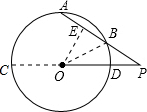 解:延长PO交⊙O与点C,过点O作OE⊥AB于E
解:延长PO交⊙O与点C,过点O作OE⊥AB于E
根据题意,∠OPA=30°,且PO=8,在Rt△OPE中,
OE=
OP=4;
在Rt△OBE中,OB=5,OE=4,
则BE=3,即AB=2BE=6;
又因为PD•PC=PB•PA,
即PD•PC=PB•(PB+AB),
即得PB=4
-3.
即AB=6;
PB=4
-3.
 解:延长PO交⊙O与点C,过点O作OE⊥AB于E
解:延长PO交⊙O与点C,过点O作OE⊥AB于E根据题意,∠OPA=30°,且PO=8,在Rt△OPE中,
OE=
| 1 |
| 2 |
在Rt△OBE中,OB=5,OE=4,
则BE=3,即AB=2BE=6;
又因为PD•PC=PB•PA,
即PD•PC=PB•(PB+AB),
即得PB=4
| 3 |
即AB=6;
PB=4
| 3 |
点评:本题综合考查了垂径定理和割线定理在圆中的应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
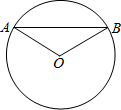 如图,⊙O的半径是4,∠AOB=120°,弦AB的长是
如图,⊙O的半径是4,∠AOB=120°,弦AB的长是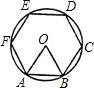 如图,⊙O的半径是6,求⊙O的内接正六边形ABCDEF的一边AB所对弧
如图,⊙O的半径是6,求⊙O的内接正六边形ABCDEF的一边AB所对弧
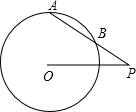 如图,⊙O的半径是5cm,P是⊙O外一点,PO=8cm,∠P=30°,则AB=
如图,⊙O的半径是5cm,P是⊙O外一点,PO=8cm,∠P=30°,则AB=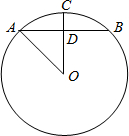 如图,⊙O的半径是10cm,弦AB的长是12cm,OC是⊙O的半径且OC⊥AB,垂足为D,则CD=
如图,⊙O的半径是10cm,弦AB的长是12cm,OC是⊙O的半径且OC⊥AB,垂足为D,则CD=