题目内容
【题目】在平面直角坐标系xOy中,A(t,0),B(t+![]() ,0),对于线段AB和点P给出如下定义:当∠APB=90°时,称点P为线段AB的“直角视点”.
,0),对于线段AB和点P给出如下定义:当∠APB=90°时,称点P为线段AB的“直角视点”.
(1)若t=﹣![]() ,在点C(0,
,在点C(0,![]() ),D(﹣1,
),D(﹣1,![]() ),E(
),E(![]() ,
,![]() )中,能够成为线段AB“直角视点”的是 .
)中,能够成为线段AB“直角视点”的是 .
(2)直线MN分别交x轴、y轴于点M、N,点M的坐标是(![]() ,0),∠OMN=30°.
,0),∠OMN=30°.
①线段AB的“直角视点”P在直线MN上,且∠ABP=60°,求点P的坐标.
②在①的条件下,记Q为直线MN上的动点,在点Q的运动过程中,△QAB的周长存在最小值,试求△QAB周长的最小值 .
③若线段AB的所有“直角视点”都在△MON内部,则t的取值范围是 .
【答案】(1)C、E;(2)①点P的坐标为 或
或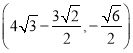 ;②
;②![]() ③
③![]()
【解析】
(1)根据给定的t值找出A、B点的坐标,再利用解三角形的方法讨论C、D、E点是否满足“直角视点”的条件即可得出结论;
(2)①分两种情况:当MN与x轴的夹角∠OMN在x轴上方时和当 MN与x轴的夹角∠OMN在x轴下方时,分别计算点P的坐标即可.
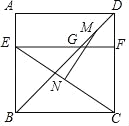
②作A关于MN的对称点A',连接BA'交MN于Q',延长AP交AB于H,H与G重合,连接AA',则AA'⊥MN,AQ'+BQ'=A'B最小,进行计算即可.
③分别计算B点与O重合,点A与M重合时t的值,从而得出线段AB的所有“直角视点”都在△MON内部,则t的取值范围.
解:(1)若![]() 则
则![]()
则![]()
∴![]()
∵点C(0,![]() ),D(﹣1,
),D(﹣1,![]() ),E(
),E(![]() ,
,![]() )
)
由勾股定理得:![]()
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴点C是线段AB的“直角视点”;
同理:
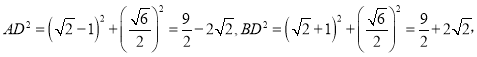
∴![]()
∴![]()
∴点D不是线段AB的“直角视点”;
同理: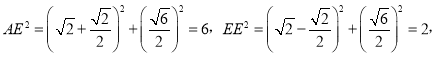
∴AE2+BE2=8=AB2,
∴∠AEB=90°,
∴点E是线段AB的“直角视点”;
故答案为:C、E;
(2)①分两种情况:当MN与x轴的夹角∠OMN在x轴上方时,
∵点P是线段AB的“直角视点”,
∴∠APB=90°,
∴点P在以AB为直径的圆上,
∵∠ABP=60°,
∴∠PAB=30°,
∴![]()
如图1所示:作PG⊥AB于G,

则![]()
∵点M的坐标是![]() ,∠OMN=30°,
,∠OMN=30°,
∴![]()
∴![]()
∴P
当MN与x轴的夹角∠OMN在x轴下方时,同理得:P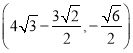
综上所述,点P的坐标为 或
或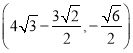 ;
;
②∵![]() ,若△QAB的周长最小,则AQ+BQ的值最小,
,若△QAB的周长最小,则AQ+BQ的值最小,
作A关于MN的对称点A',连接BA'交MN于Q',延长AP交AB于H,H与G重合,连接AA',
则AA'⊥MN,AQ'+BQ'=A'B最小,
∵∠OMN=30°,
∴∠MAA'=60°,
∵![]()
∴![]()
由勾股定理得: ![]()
∴△QAB最小值为![]()
故答案为:![]()
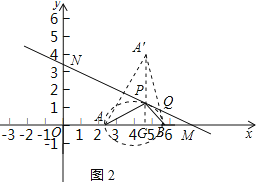
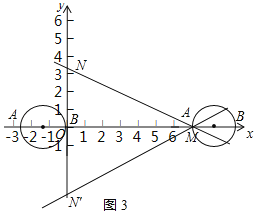
③如图3所示:
当B点与O重合,则![]()
∴![]()
当A与M重合时,![]()
∴若线段AB的所有“直角视点”都在△MON内部,t的取值范围是![]()
故答案为:![]()