题目内容
（2005•郴州）附加题：下图是由九个等边三角形组成的一个六边形，当最小的等边三角形边长为2cm时，这个六边形的周长为（ ）cm．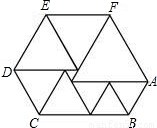
A．30
B．40
C．50
D．60
【答案】分析：因为每个三角形都是等边的，从其中一个三角形入手，比右下角的以AB为边的三角形，设它的边长为x，则等边三角形的边长依次为x，x+x+2，x+2，x+2×2，x+2×2，x+3×2．所以六边形周长是2x+2（x+2）+2（x+2×2）+（x+3×2）=7 x+18，而最大的三角形的边长AF等于AB的2倍，所以可以求出x，则可求得周长．
解答：解：设AB=x，
∴等边三角形的边长依次为x，x+x+2，x+2，x+2×2，x+2×2，x+3×2，
∴六边形周长是2x+2（x+2）+2（x+2×2）+（x+3×2）=7 x+18，
∵AF=2AB，即x+6=2x，
∴x=6cm，
∴周长为7 x+18=60cm．
故选D
点评：结合等边三角形的性质，解一元一次方程，关键是要找出其中的等量关系．
解答：解：设AB=x，
∴等边三角形的边长依次为x，x+x+2，x+2，x+2×2，x+2×2，x+3×2，
∴六边形周长是2x+2（x+2）+2（x+2×2）+（x+3×2）=7 x+18，
∵AF=2AB，即x+6=2x，
∴x=6cm，
∴周长为7 x+18=60cm．
故选D
点评：结合等边三角形的性质，解一元一次方程，关键是要找出其中的等量关系．
练习册系列答案
相关题目
＜DE＜1时，设AB与DC相交于点G（如图）．
