题目内容
(1)如图①,P为△ABC的边AB上一点(P不与点A、点B重合),连接PC,如果△CBP∽△ABC,那么就称P为△ABC的边AB上的相似点.
画法初探
①如图②,在△ABC中,∠ACB>90°,画出△ABC的边AB上的相似点P(画图工具不限,保留画图痕迹或有必要的说明);

辩证思考
②是不是所有的三角形都存在它的边上的相似点?如果是,请说明理由;如果不是,请找出一个不存在边上相似点的三角形;
特例分析
③已知P为△ABC的边AB上的相似点,连接PC,若△ACP∽△ABC,则△ABC的形状是 ;
④如图③,在△ABC中,AB=AC,∠A=36°,P是边AB上的相似点,求的值.
(2)在矩形ABCD中,AB=a,BC=b(a≥b).P是AB上的点(P不与点A、点B重合),作PQ⊥CD,垂足为Q.如果矩形ADQP∽矩形ABCD,那么就称PQ为矩形ABCD的边AB、CD上的相似线.

①类比(1)中的“画法初探”,可以提出问题:对于如图④的矩形ABCD,在不限制画图工具的前提下,如何画出它的边AB、CD上的相似线PQ呢?
你的解答是: (只需描述PQ的画法,不需在图上画出PQ).
②请继续类比(1)中的“辩证思考”、“特例分析”两个栏目对矩形的相似线进行研究,要求每个栏目提出一个问题并解决.
(1)①在∠ABC内,作∠CBD=∠A,在∠ACB内,作∠BCE=∠ABC,BD交CE于点P,则P为△ABC的自相似点;②不是,如正三角形;③直角三角形;④ ;(2)①在距离A点b2a处取点P,作PQ⊥CD,垂足为Q;②辩证思考:问题:是不是所有的矩形都存在它的边上的相似线?如果是,请说明理由;如果不是,请找出一个不存在边上相似线的矩形.解答:不是,如正方形.
;(2)①在距离A点b2a处取点P,作PQ⊥CD,垂足为Q;②辩证思考:问题:是不是所有的矩形都存在它的边上的相似线?如果是,请说明理由;如果不是,请找出一个不存在边上相似线的矩形.解答:不是,如正方形.
【解析】
试题分析:(1)①根据“自相似点”的定义结合相似三角形的判定方法求解即可;
②根据“自相似点”的定义结合相似三角形的判定方法即可作出判断;
③根据“自相似点”的定义结合相似三角形的性质即可作出判断;
④先根据等腰三角形的性质求得∠B、∠ACB的度数,再根据P是△ABC边AB上的相似点可证得△CBP∽△ABC,再根据相似三角形的性质求解即可;
(2)①在距离A点 处取点P,作PQ⊥CD,垂足为Q;
处取点P,作PQ⊥CD,垂足为Q;
②答案不唯一,合理即可.
(1)①在∠ABC内,作∠CBD=∠A,
在∠ACB内,作∠BCE=∠ABC,BD交CE于点P,
则P为△ABC的自相似点;
②不是,如正三角形.
③直角三角形.
④∵在△ABC中,AB=AC,∠A=36°,
∴∠B=∠ACB=72°.
∵P是△ABC边AB上的相似点.
∴△CBP∽△ABC.
∴∠BCP=∠A=36°,且 .
.
∴∠ACP=36°=∠A,∠B=∠BPC.
∴AP=CP=BC.
设BP=x,AP=CP=BC=y,有 =
=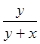 .
.
化简,得x2+xy-y2=0.
舍去负根,得 =
= ,即=
,即= ;
;
(2)①在距离A点 处取点P,作PQ⊥CD,垂足为Q;
处取点P,作PQ⊥CD,垂足为Q;
②辩证思考
问题:是不是所有的矩形都存在它的边上的相似线?如果是,请说明理由;如果不是,请找出一个不存在边上相似线的矩形.
解答:不是,如正方形.
特例分析
答案不唯一,以下答案供参考:
i)问题:已知PQ为矩形ABCD的边AB、CD上的相似线,且矩形PQCB∽矩形ABCD,a、b之间有何数量关系?
解答:a=2b.
ii)问题:已知PQ为矩形ABCD的边AB、CD上的相似线,且P 是AB的中点,a、b之间有何数量关系?
解答:a=2b.
iii)问题:已知PQ为矩形ABCD的边AB、CD上的相似线,当a=2,b=1时,求AP.
解答:AP=12.
iv)问题:已知矩形ABCD为黄金矩形(即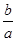 =
= ),PQ为矩形ABCD的边AB、CD上的相似线,求
),PQ为矩形ABCD的边AB、CD上的相似线,求 .
.
解答: =
= .
.
考点:相似三角形的综合题
点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案 如图,一个底角为70°的等腰三角形纸片,剪去顶角后,得到一个四边形,则∠1+∠2=
如图,一个底角为70°的等腰三角形纸片,剪去顶角后,得到一个四边形,则∠1+∠2= 如图,半径长为2的正六边形ABCDEF的顶点A在y轴上,边BC在x轴上,则点E的坐标是
如图,半径长为2的正六边形ABCDEF的顶点A在y轴上,边BC在x轴上,则点E的坐标是 如图,点P为正方形ABCD内一点,且PA=1,PB=2,PC=3.试求∠APB的度数.
如图,点P为正方形ABCD内一点,且PA=1,PB=2,PC=3.试求∠APB的度数. 如图,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于
如图,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于 如图,边长为2
如图,边长为2