��Ŀ����
����Ŀ����ͼ���ס���������������ת���ľ��ȵ�ת�̣���ת�̱��ֳ�3�������ȵ����Σ���ת�̱��ֳ�4�������ȵ����Σ�ÿһ�����ζ�������Ӧ�����֣�ͬʱת������ת�̣���ת��ֹͣ�����ת����ָ����ָ�����ڵ�����Ϊm����ת����ָ����ָ�����ڵ�����Ϊn(��ָ��ָ�ڱ߽�����ʱ����תһ�Σ�ֱ��ָ�붼ָ��һ������Ϊֹ)��
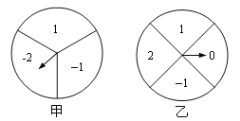
��1�������û���״ͼ���б���ķ������|m��n|��1�ĸ��ʣ�
��2��ֱ��д����(m��n)���ں���y���� ͼ���ϵĸ��ʣ�
���𰸡�
��1���������£�
����ת���� | -1 | 0 | 1 | 2 |
ת�̼� | ||||
-1 | ��-1��-1�� | ��-1��0�� | ��-1��1�� | ��-1��2�� |
-2 | ��-2��-1�� | ��-2��0�� | ��-2��1�� | ��-2��2�� |
1 | ��1��-1�� | ��1��0�� | ��1��1�� | ��1��2�� |
��6�֣�
�ɱ����֪�����еȿ��ܵĽ����12�֣�����|m+n|��1�������5�֣���7�֣�
����|m+n|��1�ĸ���ΪP1=![]() ����8�֣�
����8�֣�
��2���㣨m��n���ں���y=-![]() �ϵĸ���ΪP2=
�ϵĸ���ΪP2=![]() =
=![]() ����10�֣�
����10�֣�
����������1�����������б���Ȼ������б�������п��ܵĽ����|m+n|��1����������ݸ��ʹ�ʽ��⼴�ɣ�
��2�����ݣ�1���е���״ͼ��������õ㣨m��n�����ں���y=-ͼ���ϵ�������ɸ��ʹ�ʽ������ô𰸣�