题目内容
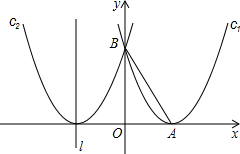 已知,如图所示,抛物线c1:y=ax2+bx+c的顶点A在x轴的正半轴上,并与y轴交于点B,OA=
已知,如图所示,抛物线c1:y=ax2+bx+c的顶点A在x轴的正半轴上,并与y轴交于点B,OA=| 3 |
| 3 |
(1)求抛物线c1的函数解析式,并直接写出抛物线c2的函数解析式;
(2)设l是抛物线c2的对称轴,P是l上的一点,求当△PAB的周长最小时点P的坐标;
(3)在抛物线c1上是否存在点D,过点D作DC⊥AB于C,使得△DCB与△AOB相似?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
分析:(1)在Rt△OAB中OA=
,AB=2
,求得OB的长,从而根据OA,OB得到点A,D坐标,点A坐标即为其顶点坐标,从而得到C1,C2C1关于原点对称,从而得到C2的顶点坐标,即其对称轴,从而得到C2解析式.
(2)作BB′∥x轴交C2于点B′则点B′即为点B关于l的对称点,连接AB′交l于点P即为所求点.先求得直线AB′,代入对称轴l的x值,从而进一步求得点P.
(3)设点设点D(x,(x-
)2),求得BD,求得直线AB,求得点D到直线AB的距离,若△DCB与△AOB相似,则
=
或
=
,代入求得的等式是否是否符合,符合则点D存在.
| 3 |
| 3 |
(2)作BB′∥x轴交C2于点B′则点B′即为点B关于l的对称点,连接AB′交l于点P即为所求点.先求得直线AB′,代入对称轴l的x值,从而进一步求得点P.
(3)设点设点D(x,(x-
| 3 |
| BD |
| AB |
| CD |
| OB |
| BD |
| AB |
| CD |
| OA |
解答:解:(1)∵在Rt△OAB中OA=
,AB=2
,
∴OB=
=3,
∴点A(
,0),点B(0,3).
则由
,
解得:a=1,b=-2
,c=3,
∴C1的解析式为:y=x2-2
x+3=(x-
)2.
则点A关于y轴的对称点为(-
,0),
相当于C1向左平移了2
个单位,
∴C2的解析式为:y=(x+
)2;
(2)作BB′∥x轴交C2于点B′则点B′即为点B关于l的对称点,连接AB′交l于点P即为所求点.
此时AB′即为△APB所形成三角形的最小周长.两点之间线段最短.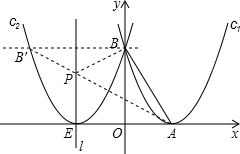
∵点A(
,0),点B(0,3),
∴E(-
,0),
∴B′(-2
,3),
则设直线AB′为y=kx+b,代入A,B′得:
.
解得:k=-
,b=1,
∴直线AB′解析式为:y=-
x+1,
代入对称轴x=-
,则y=2,
∴点P(-
,2);
(3)如图:存在,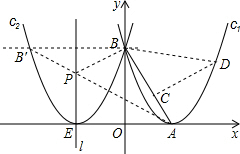
知道点A,B设直线AB为y=mx+n,
代入解得:y=-
x+3,即y+
x-3=0,
设点D(x,(x-
)2),则BD=
,
则点D到直线的距离CD.
知道OA=
,OB=3,AB=2
,
若△DCB与△AOB相似,则
=
或
=
,
代入
=
,
则点D(1,4-2
),
检验点D符合,
代入
=
,
则点D(3,12-6
),
检验符合,
∴点D(1,4-2
)或(3,12-6
).
| 3 |
| 3 |
∴OB=
| AB2-OA2 |
∴点A(
| 3 |
则由
|
解得:a=1,b=-2
| 3 |
∴C1的解析式为:y=x2-2
| 3 |
| 3 |
则点A关于y轴的对称点为(-
| 3 |
相当于C1向左平移了2
| 3 |
∴C2的解析式为:y=(x+
| 3 |
(2)作BB′∥x轴交C2于点B′则点B′即为点B关于l的对称点,连接AB′交l于点P即为所求点.
此时AB′即为△APB所形成三角形的最小周长.两点之间线段最短.

∵点A(
| 3 |
∴E(-
| 3 |
∴B′(-2
| 3 |
则设直线AB′为y=kx+b,代入A,B′得:
|
解得:k=-
| ||
| 3 |
∴直线AB′解析式为:y=-
| ||
| 3 |
代入对称轴x=-
| 3 |
∴点P(-
| 3 |
(3)如图:存在,

知道点A,B设直线AB为y=mx+n,
代入解得:y=-
| 3 |
| 3 |
设点D(x,(x-
| 3 |
2x2-2
|
则点D到直线的距离CD.
知道OA=
| 3 |
| 3 |
若△DCB与△AOB相似,则
| BD |
| AB |
| CD |
| OB |
| BD |
| AB |
| CD |
| OA |
代入
| BD |
| AB |
| CD |
| OB |
则点D(1,4-2
| 3 |
检验点D符合,
代入
| BD |
| AB |
| CD |
| OA |
则点D(3,12-6
| 3 |
检验符合,
∴点D(1,4-2
| 3 |
| 3 |
点评:本题考查了二次函数的综合运用,涉及到知道抛物线上的点求其解析式,求抛物线的对称轴,以及抛物线的平移.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
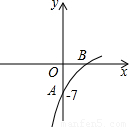
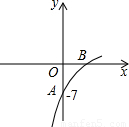
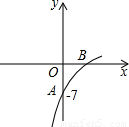
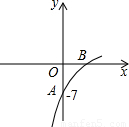
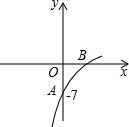 已知抛物线y=(1-a)x2+8x+b的图象的一部分如图所示,抛物的顶点在第一象限,且经过点A(0,-7)和点B.
已知抛物线y=(1-a)x2+8x+b的图象的一部分如图所示,抛物的顶点在第一象限,且经过点A(0,-7)和点B.