Question

某体育器材专卖柜经销A、B两种器材，A种器材每件进价350元，售价480元；B种器材每件进价200元，售价300元．
（1）该专卖柜计划用8000元去购进A、B两种器材若干件．
①若购进A种器材x件，B种器材y件，所获利润w元，请写出w与x之间的函数关系式；
②怎样购进才能使专卖柜经销这两种器材所获利润最大（其中A种器材不少于7件）？
（2）在“五•一”期间，该专卖柜对A、B两种器材进行如下优惠促销活动：

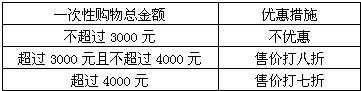
一次项购物总金额	优惠措施
不超过3000元	不优惠
超过3000元不超过4000元	售价打八折
超过4000元	售价打七折

促销活动期间：甲学校去该专卖柜购买A种器材付款2688元；乙学校去该专卖柜购买B种器材付款2100元；丙学校决定一次性购买甲学校和乙学校购买的同样多的器材需付款多少元？

Answer 1

【答案】分析：（1）①由350x+200y=8000，w=（480-350）x+（300-200）y可得到w和x的关系表达式；
②由上面w和x的关系表达式可得到当x≥7时w最大值；
（2）分别求出甲学校和乙学校所买器材数，再根据题中打折情况求出丙学校购买相同器材所需付款．
解答：解：（1）由题意可得：
350x+200y=8000，
∴100y=4000-175x．
而w=（480-350）x+（300-200）y=130x+100y，
将100y=4000-175x代入上式得：
w=-45x+4000；

（2）由w=-45x+4000知w是x的一次函数，随x的增大而减少，
又∵x是大于等于7的整数，且y也为整数，
∴当x=8时，w最大，此时y=26
所以购进A器材8件，购进B器材26件才能使超市经销这两种器材所获利润最大．

（3）∵3000×0.8=2400，4000×0.7=2800，
而2100＜2400＜2688＜2800，
∴乙学校去该专卖柜购买B种器材：2100÷300=7（件）．
甲学校去该专卖柜购买A种器材：2688÷0.8÷480=7（件）．
∴丙学校一次去购买甲学校和乙学校购买的同样多的器材：
7×350+7×480=5810＞4000．
丙学校付款为：5810×0.7=4067（元）
故丙学校付款4067元．
点评：本题考查的是用一次函数解决实际问题，此类题是近年中考中的热点问题．注意利用一次函数求最值时，关键是应用一次函数的性质．