题目内容
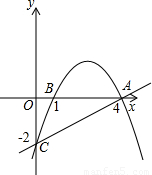
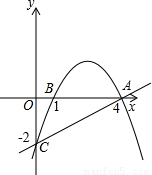
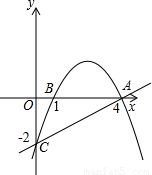
(2009•临沂)如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.(1)求出抛物线的解析式;
(2)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
(3)在直线AC上方的抛物线上有一点D,使得△DCA的面积最大,求出点D的坐标.
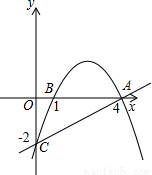
【答案】分析:(1)已知抛物线经过A(4,0),B(1,0),可设抛物线解析式的交点式,再把C(0,-2)代入即可;
(2)∵△OAC是直角三角形,以A,P,M为顶点的三角形与其相似,由于点P可能在x轴的上方,或者下方,分三种情况,分别用相似比解答;
(3)过D作y轴的平行线交AC于E,将△DCA分割成两个三角形△CDE,△ADE,它们的底相同,为DE,高的和为4,就可以表示它们的面积和,即△DCA的面积,运用代数式的变形求最大值.
解答:解:(1)∵该抛物线过点C(0,-2),
设该抛物线的解析式为y=ax2+bx-2.
将A(4,0),B(1,0)代入,
得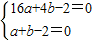 ,
,
解得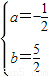 ,
,
∴此抛物线的解析式为y=- x2+
x2+ x-2.
x-2.
(2)存在.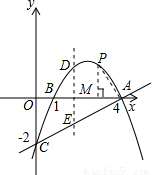
如图,设P点的横坐标为m,
则点P的纵坐标为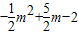 ,
,
当1<m<4时,
AM=4-m,PM=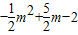 ,
,
又∵∠COA=∠PMA=90°,
∴①当 =
=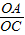 =2时,△APM∽△ACO,
=2时,△APM∽△ACO,
∴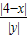 =2,即|4-m|=2(
=2,即|4-m|=2(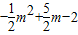 ),
),
∴4-m=m2+5m-4,
∴m2-6m+8=0,
∴(m-2)(m-4)=0,
解得:m1=2,m2=4(舍去)
∴P(2,1)
②当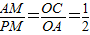 ,△APM∽△CAO,
,△APM∽△CAO,
那么有:2|4-m|=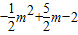 ,
,
∴2(4-m)=- m2+
m2+ m-2,
m-2,
∴m2-9m+20=0,
∴(m-4)(m-5)=0,
解得:m1=4(舍去),m2=5(舍去),
∴当1<m<4时,P(2,1),
类似地可求出当m>4时,P(5,-2),
当m<1时,P(-3,-14),
当P,C重合时,△APM≌△ACO,P(0,-2).
综上所述,符合条件的点P为(2,1)或(5,-2)或(-3,-14)或(0,-2);
(3)如图,设D点的横坐标为t(0<t<4),则D点的纵坐标为- t2+
t2+ t-2.
t-2.
过D作y轴的平行线交AC于E.
由题意可求得直线AC的解析式为y= x-2.
x-2.
∴E点的坐标为(t, t-2).
t-2).
∴DE=- t2+
t2+ t-2-(
t-2-( t-2)=-
t-2)=- t2+2t.
t2+2t.
∴S△DAC= ×(-
×(- t2+2t)×4=-t2+4t=-(t-2)2+4.
t2+2t)×4=-t2+4t=-(t-2)2+4.
∴当t=2时,△DAC面积最大.
∴D(2,1).
点评:本题综合考查了抛物线解析式的求法,抛物线与相似三角形的问题,坐标系里表示三角形的面积及其最大值问题,要求会用字母代替长度,坐标,会对代数式进行合理变形.
(2)∵△OAC是直角三角形,以A,P,M为顶点的三角形与其相似,由于点P可能在x轴的上方,或者下方,分三种情况,分别用相似比解答;
(3)过D作y轴的平行线交AC于E,将△DCA分割成两个三角形△CDE,△ADE,它们的底相同,为DE,高的和为4,就可以表示它们的面积和,即△DCA的面积,运用代数式的变形求最大值.
解答:解:(1)∵该抛物线过点C(0,-2),
设该抛物线的解析式为y=ax2+bx-2.
将A(4,0),B(1,0)代入,
得
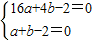 ,
,解得
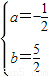 ,
,∴此抛物线的解析式为y=-
 x2+
x2+ x-2.
x-2.(2)存在.

如图,设P点的横坐标为m,
则点P的纵坐标为
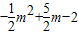 ,
,当1<m<4时,
AM=4-m,PM=
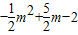 ,
,又∵∠COA=∠PMA=90°,
∴①当
 =
=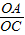 =2时,△APM∽△ACO,
=2时,△APM∽△ACO,∴
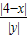 =2,即|4-m|=2(
=2,即|4-m|=2(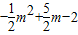 ),
),∴4-m=m2+5m-4,
∴m2-6m+8=0,
∴(m-2)(m-4)=0,
解得:m1=2,m2=4(舍去)
∴P(2,1)
②当
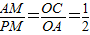 ,△APM∽△CAO,
,△APM∽△CAO,那么有:2|4-m|=
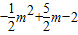 ,
,∴2(4-m)=-
 m2+
m2+ m-2,
m-2,∴m2-9m+20=0,
∴(m-4)(m-5)=0,
解得:m1=4(舍去),m2=5(舍去),
∴当1<m<4时,P(2,1),
类似地可求出当m>4时,P(5,-2),
当m<1时,P(-3,-14),
当P,C重合时,△APM≌△ACO,P(0,-2).
综上所述,符合条件的点P为(2,1)或(5,-2)或(-3,-14)或(0,-2);
(3)如图,设D点的横坐标为t(0<t<4),则D点的纵坐标为-
 t2+
t2+ t-2.
t-2.过D作y轴的平行线交AC于E.
由题意可求得直线AC的解析式为y=
 x-2.
x-2.∴E点的坐标为(t,
 t-2).
t-2).∴DE=-
 t2+
t2+ t-2-(
t-2-( t-2)=-
t-2)=- t2+2t.
t2+2t.∴S△DAC=
 ×(-
×(- t2+2t)×4=-t2+4t=-(t-2)2+4.
t2+2t)×4=-t2+4t=-(t-2)2+4.∴当t=2时,△DAC面积最大.
∴D(2,1).
点评:本题综合考查了抛物线解析式的求法,抛物线与相似三角形的问题,坐标系里表示三角形的面积及其最大值问题,要求会用字母代替长度,坐标,会对代数式进行合理变形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目