题目内容
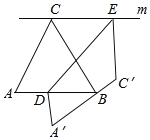
【题目】如图,△ABC是边长为1的等边三角形,过点C的直线m平行AB,D、E分别是线段AB、直线m上的点,先按如图方式进行折叠,点A、C分别落在A′、C′处,且A′C′经过点B,DE为折痕,当C′E⊥m时,![]() 的值为_____.
的值为_____.
【答案】1+![]()
【解析】
由折叠的性质得出∠C′ED=∠CED=45°,由平行线的性质得出∠BDE=∠DEC=45°,再由等边三角形的性质得出AB=AC=1,∠A=∠ABC=∠ACB=60°,求出∠DFB=∠CFE=75°,得出∠BCE=60°,∠ACE=∠C′=120°,证出∠A′DB=90°,由直角三角形的性质得出A′B=2A′D,设AD=x,则BA′=2x,BD=1-x,A′D=x,BC′=1-2x,在Rt△A′BD中,由勾股定理得出方程,解方程求出x的值,即可得出结果.
∵C′E⊥m,
∴∠CEC′=90°,
∵DE为折痕,
∴∠C′ED=∠CED=45°,
∵m∥AB,
∴∠BDE=∠DEC=45°,
∵△ABC是等边三角形,
∴AB=AC=1,∠A=∠ABC=∠ACB=60°,
设CB与DE交于点F,如图所示:
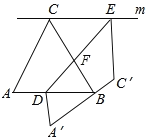
则∠DFB=∠CFE=75°,
∴∠BCE=60°,
∴∠ACE=∠C′=120°,
∵∠A=∠A′=60°,
∴∠A′DE=135°,
∴∠A′DB=90°,
∴A′B=2A′D,
∵A′D=AD,
设AD=x,则BA′=2x,BD=1﹣x,A′D=x,BC′=1﹣2x,
在Rt△A′BD中,由勾股定理得:x2+(1﹣x)2=(2x)2,
解得:x=![]() (负值舍去),
(负值舍去),
∴x=![]() ,
,
∴BA'=﹣1+![]() ,BC'=1﹣(﹣1+
,BC'=1﹣(﹣1+![]() )=2﹣
)=2﹣![]() ,
,
∴![]() =
=![]() =1+
=1+![]() ;
;
故答案为:1+![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目