题目内容
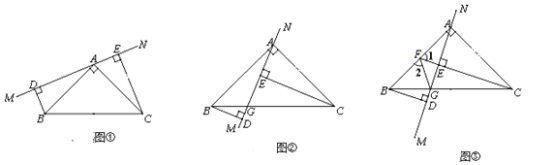
【题目】如图①，在
中， 
， 
， 
． 
是经过点
的直线， 
于
， 
于
．
（1）求证： 
．
（2）若将
绕点
旋转，使
与
相交于点
(如图②)，其他条件不变，
求证： 
．
（3）在(2)的情况下，若
的延长线过
的中点
（如图③），连接
，
求证： 
．
【答案】答案见解析
【解析】试题分析：（1）首先证明∠DBA＝∠EAC，再证明△ADB≌△CEA，然后根据全等三角形的性质可得BD=AE；
（2）首先证明∠BAD=∠ACE，再证明△ABD≌△ACE，根据全等三角形对应边相等可得BD=AE；
（3）首先证明△ACF≌△ABP，然后再证明△BFG≌△BPG，再根据全等三角形对应角相等可得∠BPG=∠BFG，再根据等量代换可得结论∠1=∠2．
试题解析：
（1）∵BD⊥MN，CE⊥MN
∴∠BDA＝∠AEC＝90°
∴∠DBA+∠DAB＝90°
∵∠BAC＝90°
∴∠DAB +∠EAC＝90°
∴∠DBA＝∠EAC
∵AB = AC
∴△ADB≌△CEA（AAS）
∴BD＝AE
（2）∵BD⊥MN，CE⊥MN
∴∠BDA＝∠AEC＝90°
∴∠DBA+∠DAB＝90°
∵∠BAC＝90°
∴∠DAB +∠EAC＝90°
∴∠DBA＝∠EAC
∵AB = AC
∴△ADB≌△CEA（AAS）
∴BD＝AE
（3）过B作BP//AC交MN于P,如图所示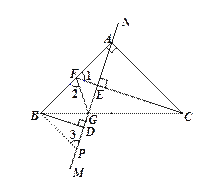
∵BP//AC
∴∠PBA+∠BAC＝90°
∵∠BAC＝90°
∴∠PBA＝∠BAC＝90°
由（2）得：△ADB≌△CEA
∴∠BAP＝∠ACF
∵AB＝AC
∴△ACF≌△ABP（ASA）
∴∠1＝∠3
∴AF=BP
∵AB的中点F
∵BF＝AF
∴BF＝BP
∵∠ABC=45°
又∵∠PBA＝90°
∴∠PBG＝∠PBA－∠ABC =45°
∴∠ABC＝∠PBG
∵BG=BG
∴△BFG≌△BPG（SAS）
∴∠2＝∠3
∵∠1＝∠3
∴∠1＝∠2
