题目内容
如果x,y满足不等式组 ,那么你能画出点(x,y)所在的平面区域吗?
,那么你能画出点(x,y)所在的平面区域吗?
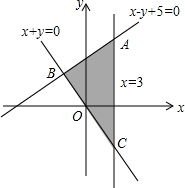 解:如图所示:在直角坐标系画出直线x=3,x+y=0,x-y+5=0,
解:如图所示:在直角坐标系画出直线x=3,x+y=0,x-y+5=0,∵原点(0,0)不在直线x-y+5=0上,
∴将原点(0,0)代入x-y+5可知,原点所在平面区域表示x-y+5≥0部分,
∵原点在直线x+y=0上,
∴取点(0,1)代入x+y判定可知点(0,1)所在平面区域表示x+y≥0的部分.
分析:在直角坐标系画出直线x=3,x+y=0,x-y+5=0,因为原点(0,0)不在直线x-y+5=0上,
故将原点(0,0)代入x-y+5可知,原点所在平面区域表示x-y+5≥0部分,因为原点在直线x+y=0上,故取点(0,1)代入x+y判定可知点(0,1)所在平面区域表示x+y≥0的部分.
点评:本题考查的是一次函数与一元一次不等式,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
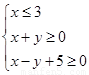 ,那么你能画出点(x,y)所在的平面区域吗?
,那么你能画出点(x,y)所在的平面区域吗?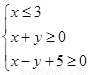 ,那么你能画出点(x,y)所在的平面区域吗?
,那么你能画出点(x,y)所在的平面区域吗?