Question

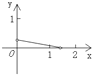
【题目】已知一次函数的图象交轴和轴于点和；另一个一次函数的图象交轴和轴于点和，且两个函数的图象交于点

（1）当，为何值时，和的图象重合；

（2）当的面积为时，求线段的长．

Answer 1

【答案】（1）a=2，b=2；（2）ED=2或8．

【解析】

（1）把A（1，4）代入y1=ax+b求得a+b=4，得到b=4-a，于是得到结论；

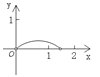
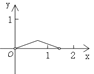
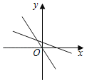
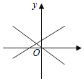
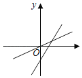
（2）根据题意，需要分成两种情况进行第一种情况，如图2，第二种情况，如图3，根据函数解析式得到B，C，D，E，求得BC的长度，根据三角形的面积列方程即可得到结论．

解：（1）∵的图象过点，

∴a+b=4，

∴b=4-a，

∴y1=ax+（4-a），y2=（4-a）x+a，

∵y1和y2的图象重合，

∴a=4-a，

∴a=2，b=2；

即当a=2，b=2时，y1和y2的图象重合；

（2）第一种情况，如图2，

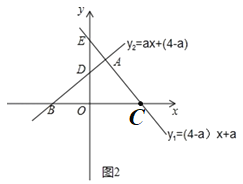
根据题意易求得：B（，0），C（，0），D（0，），E（0，a），

∴，

∵

∴

解得：或；

经检验，，是原分式方程的解；

∴，，，，

∴，；

第二种情况，如图3：

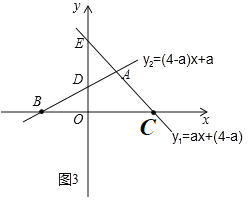
∵B（，0），C（，0），D（0，），E（0，），

∴，

∴

解得：或，

经检验，，是原分式方程的解；

∴，，，，

∴，；

综上所述，或．