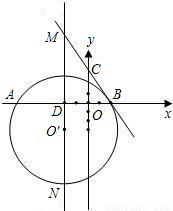
题目内容
(2006•巴中)如图,在平面直角坐标系中,以点0′(-2,-3)为圆心,5为半径的圆交x轴于A、B两点,过点B作⊙O′的切线,交y轴于点C,过点0′作x轴的垂线MN,垂足为D,一条抛物线(对称轴与y轴平行)经过A、B两点,且顶点在直线BC上.(1)求直线BC的解析式;
(2)求抛物线的解析式;
(3)设抛物线与y轴交于点P,在抛物线上是否存在一点Q,使四边形DBPQ为平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.

【答案】分析:(1)求直线BC的解析式,首先要求出的是B、C的坐标,即OB、OC的长;连接O′B,在直角三角形O′DB中可根据O′D及半径的长用勾股定理求出DB的长,然后根据OD的长即O′横坐标的绝对值求出OB的长,即可求出B的坐标.求OC长,可根据△BOC∽△O′DB得出的比例线段来求出.求出B、C的坐标后,可用待定系数法求出直线BC的解析式.
(2)由于抛物线过A、B两点,根据抛物线的对称性进可得出抛物线的对称轴为x=-2,又已知抛物线的顶点在直线BC上,由此可求出抛物线顶点的坐标.然后用顶点式的二次函数通式来设抛物线的解析式,然后将B点坐标代入即可求出抛物线的解析式.
(3)可根据(2)得出的抛物线的解析式,求出P点的坐标.由于四边形DBPQ为平行四边形,那么DP平行且相等于DB,因此可将P点坐标左移DB长即4个单位,即可得出Q点,然后将Q点坐标代入抛物线的解析式中即可判断出Q点是否在抛物线上.
解答:解:(1)连接O′B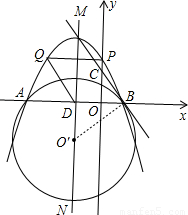
∵O′(-2,-3),MN过点O′且与x轴垂直
∴O′D=3,OD=2,AD=BD= AB
AB
∵⊙O′的半径为5
∴BD=AD=4
∴OA=6,OB=2
∴点A、B的坐标分别为(-6,0)、(2,0)
∵BC切⊙O′于B
∴O′B⊥BC
∴∠OBC+∠O′BD=90°
∵∠O′BD+∠BO′D=90°
∴∠OBC=∠BO′D
∵∠BOC=∠BDO′=90°
∴△BOC∽△O′DB
∴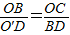
∴OC=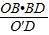 =
=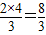
∴点C的坐标为(0, )
)
设直线BC的解析式为y=kx+b
∴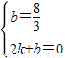
解得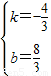
∴直线BC的解析式为y=- x+
x+ ;
;
(2)由圆和抛物线的对称性可知MN是抛物线的对称轴,
∴抛物线顶点的横坐标为-2
∵抛物线的顶点在直线y=- x+
x+ 上
上
∴y=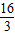 即抛物线的顶点坐标为(-2,
即抛物线的顶点坐标为(-2,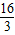 )
)
设抛物线的解析式为y=a(x+6)(x-2)
得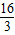 =a(-2+6)(-2-2)
=a(-2+6)(-2-2)
解得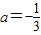
∴抛物线的解析式为y=- (x+6)(x-2)=-
(x+6)(x-2)=- x2-
x2- x+4;
x+4;
(3)由(2)得抛物线与y轴的交点P的坐标为(0,4),
若四边形DBPQ是平行四边形,
则有BD∥PQ,BD=PQ,
∴点Q的纵坐标为4
∵BD=4
∴PQ=4
∴点Q的横坐标为-4
∴点Q的坐标为(-4,4)
∴当x=-4时,y=- x2-
x2- x+4=-
x+4=- ×16+
×16+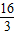 +4=4
+4=4
∴点Q在抛物线上
∴在抛物线上存在一点Q(-4,4),使四边形DBPQ为平行四边形.
点评:本题考查了待定系数法求二次函数解析式、三角形相似、平行四边形的判定等知识点,综合性强,考查学生数形结合的数学思想方法.
(2)由于抛物线过A、B两点,根据抛物线的对称性进可得出抛物线的对称轴为x=-2,又已知抛物线的顶点在直线BC上,由此可求出抛物线顶点的坐标.然后用顶点式的二次函数通式来设抛物线的解析式,然后将B点坐标代入即可求出抛物线的解析式.
(3)可根据(2)得出的抛物线的解析式,求出P点的坐标.由于四边形DBPQ为平行四边形,那么DP平行且相等于DB,因此可将P点坐标左移DB长即4个单位,即可得出Q点,然后将Q点坐标代入抛物线的解析式中即可判断出Q点是否在抛物线上.
解答:解:(1)连接O′B

∵O′(-2,-3),MN过点O′且与x轴垂直
∴O′D=3,OD=2,AD=BD=
 AB
AB∵⊙O′的半径为5
∴BD=AD=4
∴OA=6,OB=2
∴点A、B的坐标分别为(-6,0)、(2,0)
∵BC切⊙O′于B
∴O′B⊥BC
∴∠OBC+∠O′BD=90°
∵∠O′BD+∠BO′D=90°
∴∠OBC=∠BO′D
∵∠BOC=∠BDO′=90°
∴△BOC∽△O′DB
∴
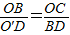
∴OC=
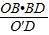 =
=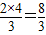
∴点C的坐标为(0,
 )
)设直线BC的解析式为y=kx+b
∴
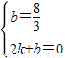
解得
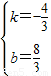
∴直线BC的解析式为y=-
 x+
x+ ;
;(2)由圆和抛物线的对称性可知MN是抛物线的对称轴,
∴抛物线顶点的横坐标为-2
∵抛物线的顶点在直线y=-
 x+
x+ 上
上∴y=
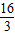 即抛物线的顶点坐标为(-2,
即抛物线的顶点坐标为(-2,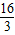 )
)设抛物线的解析式为y=a(x+6)(x-2)
得
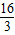 =a(-2+6)(-2-2)
=a(-2+6)(-2-2)解得
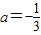
∴抛物线的解析式为y=-
 (x+6)(x-2)=-
(x+6)(x-2)=- x2-
x2- x+4;
x+4;(3)由(2)得抛物线与y轴的交点P的坐标为(0,4),
若四边形DBPQ是平行四边形,
则有BD∥PQ,BD=PQ,
∴点Q的纵坐标为4
∵BD=4
∴PQ=4
∴点Q的横坐标为-4
∴点Q的坐标为(-4,4)
∴当x=-4时,y=-
 x2-
x2- x+4=-
x+4=- ×16+
×16+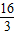 +4=4
+4=4∴点Q在抛物线上
∴在抛物线上存在一点Q(-4,4),使四边形DBPQ为平行四边形.
点评:本题考查了待定系数法求二次函数解析式、三角形相似、平行四边形的判定等知识点,综合性强,考查学生数形结合的数学思想方法.

练习册系列答案
相关题目