题目内容
在等腰三角形ABC中，AB=AC，其一腰上的高为h。 M是底边BC上的任意一点，M到腰AB、AC的距离分别为h1、h2
（1）请你结合图形1来证明：h1+h2=h
（1）请你结合图形1来证明：h1+h2=h
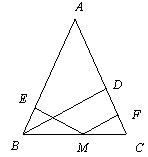
（2）当点M在BC延长线上时，h1、h2、h之间又有什么样的结论，请你画出图形，并直接写出结论不必证明。
（3）利用以上结论解答，如图2在平面直角坐标系中有两条直线l1：y=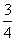
x+3 , l2：y=-3x+3，若l2上的一点M到l1的距离是
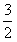，求点M的坐标。
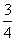x+3 , l2：y=-3x+3，若l2上的一点M到l1的距离是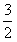，求点M的坐标。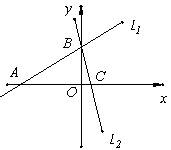 
解：（1）证明“略”
（2） 画图“略”，h1-h2=h
（3）解AC=5 ，所以AB=AC，即△ABC为等腰三角形
（ⅰ）当点M在BC边上时，由h1+h2=h求得此时M（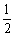
，
）
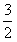（ⅱ）当点M在CB延长线上时，由h1-h2=h求得此时M（-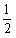
，
）
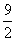综合（ⅰ）、（ⅱ）知：点M的坐标为 M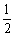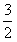（，）或（-，）
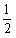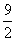（2） 画图“略”，h1-h2=h
（3）解AC=5 ，所以AB=AC，即△ABC为等腰三角形
（ⅰ）当点M在BC边上时，由h1+h2=h求得此时M（
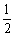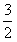，）（ⅱ）当点M在CB延长线上时，由h1-h2=h求得此时M（-
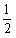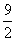，） 综合（ⅰ）、（ⅱ）知：点M的坐标为 M（
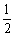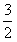，）或（-，）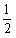
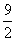练习册系列答案
相关题目
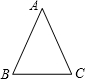如图：在等腰三角形ABC中，AB=AC，∠A=40°，则∠B=
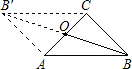在等腰三角形ABC中，∠C=90°，BC=2cm．如果以AC的中点O为旋转中心，将这个三角形旋转180°，点B落在点B′处，那么点B′与点B的原来位置相距
如图所示，在等腰三角形ABC中，AB=AC=13cm，底边BC=10cm，求底边上的高AD和△ABC的面积．
如图，在等腰三角形ABC中，两底角的平分线BE和CD相交于点0，则△OBC是