题目内容
（2012•内江）如图，四边形ABCD是梯形，BD=AC且BD⊥AC，若AB=2，CD=4，则S梯形ABCD=9
9
．分析：过点B作BE∥AC交DC的延长线于点E，过点B作BF⊥DC于点F，判断出△BDE是等腰直角三角形，求出BF，继而利用梯形的面积公式即可求解．
解答：
解：过点B作BE∥AC交DC的延长线于点E，过点B作BF⊥DC于点F，
则AC=BE，DE=DC+CE=DC+AB=6，
又∵BD=AC且BD⊥AC，
∴△BDE是等腰直角三角形，
∴BF=
DE=3，
故可得梯形ABCD的面积为
（AB+CD）×BF=9．
故答案为：9．
解：过点B作BE∥AC交DC的延长线于点E，过点B作BF⊥DC于点F，则AC=BE，DE=DC+CE=DC+AB=6，
又∵BD=AC且BD⊥AC，
∴△BDE是等腰直角三角形，
∴BF=
| 1 |
| 2 |
故可得梯形ABCD的面积为
| 1 |
| 2 |
故答案为：9．
点评：此题考查了梯形的知识，平移一条对角线是经常用到的一种辅助线的作法，同学们要注意掌握，解答本题也要熟练等腰直角三角形的性质，难度一般．
练习册系列答案
相关题目
（2012•内江）如图所示，△ABC的顶点是正方形网格的格点，则sinA的值为（ ）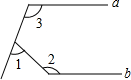
（2012•内江）如图，a∥b，∠1=65°，∠2=140°，则∠3=（ ）
（2012•内江）如图所示，A、B是边长为1的小正方形组成的网格的两个格点，在格点中任意放置点C，恰好能使△ABC的面积为1的概率是
（2012•内江）如图，四边形ABCD是矩形，E是BD上的一点，∠BAE=∠BCE，∠AED=∠CED，点G是BC、AE延长线的交点，AG与CD相交于点F．