题目内容
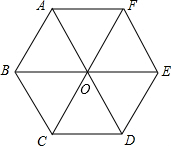 如图,正六边形ABCDEF是由边长为2厘米的六个等边三角形拼成,那么图中:
如图,正六边形ABCDEF是由边长为2厘米的六个等边三角形拼成,那么图中:(1)三角形AOB沿着
射线BO
射线BO
方向平移2
2
厘米能与三角形FEO重合;(2)三角形AOB绕着点
O
O
顺时针旋转120
120
度后能与三角形EOF重合;(3)三角形AOB沿着BE所在直线翻折后能与
△CBO
△CBO
重合;(4)写一对中心对称的三角形:
△AOB与△DOE
△AOB与△DOE
.分析:(1)结合图形可判断平移距离为OE的长度;
(2)根据旋转的定义,结合图形可得出答案.
(3)根据轴对称的定义,结合图形可得出翻折后与△CBO重合.
(4)根据中心对称的定义,结合图形写出一对即可.
(2)根据旋转的定义,结合图形可得出答案.
(3)根据轴对称的定义,结合图形可得出翻折后与△CBO重合.
(4)根据中心对称的定义,结合图形写出一对即可.
解答:解:(1)三角形AOB沿着射线BO方向平移2厘米能与三角形FEO重合;
(2)三角形AOB绕着点O顺时针旋转120度后能与三角形EOF重合;
(3)三角形AOB沿着BE所在直线翻折后能与△CBO重合;
(4)△AOB与△DOE是中心对称的两个三角形.
故答案为:射线BO、2厘米;O、120;△COB;△AOB与△DOE.
(2)三角形AOB绕着点O顺时针旋转120度后能与三角形EOF重合;
(3)三角形AOB沿着BE所在直线翻折后能与△CBO重合;
(4)△AOB与△DOE是中心对称的两个三角形.
故答案为:射线BO、2厘米;O、120;△COB;△AOB与△DOE.
点评:此题考查了几何变换的类型,属于基础题,关键是掌握几种变换的定义和特点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
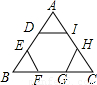
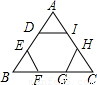
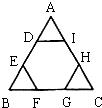 18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是
18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是