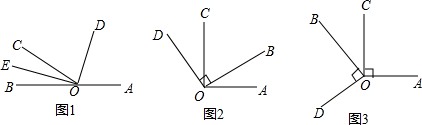
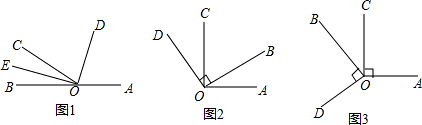
题目内容
①如图1,已知射线OC在平角∠AOB的内部,且∠AOC>∠BOC,OD平分∠AOC,OE平分∠BOC.
(1)比较∠COD与∠COE的大小,并说明理由.
(2)你能求出∠DOE的大小吗?如果能,请求出它的度数,若不能,说明理由.
(3)若∠AOB=a,你能用a表示∠DOE的度数吗?请说明理由.
②如图2,∠AOC与∠BOD都是直角,∠BOC=50°.
(1)求∠AOB和∠DOC的度数,∠AOB和∠DOC有何大小关系?
(2)若∠BOC的具体度数不稳定,其他条件不变,这种关系仍然成立吗?说明理由.
(3)试猜想∠AOD与∠COB在数量上是相等、互余,还是互补关系?你能用推理的方法说明你的猜想是否合理吗?
(4)当∠BOD绕点O旋转到图3位置时,你原来的猜想还成立吗?说明理由.
(1)解:∠COD>∠COE,
理由是:∵OD平分∠AOC,OE平分∠BOC,
∴∠COD= ∠AOC,∠COE=
∠AOC,∠COE= ∠BOC,
∠BOC,
∵∠AOC>∠BOC,
∴∠COD>∠COE;
(2)解:能求出∠DOE的度数,是90°,
理由是:∠DOE= (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ∠AOB=
∠AOB= ×180°=90°.
×180°=90°.
(3)解:能,∠DOE= α,
α,
理由是:∵∠AOB=∠AOC+∠BOC=α,
∵OD平分∠AOC,OE平分∠BOC,
∴∠COD= ∠AOC,∠COE=
∠AOC,∠COE= ∠BOC,
∠BOC,
∴∠DOE= ∠AOB=
∠AOB= α.
α.
分析:(1)根据角平分线性质推出∠COD= ∠AOC,∠COE=
∠AOC,∠COE= ∠BOC,再根据已知求出即可;
∠BOC,再根据已知求出即可;
(2)根据∠COD= ∠AOC,∠COE=
∠AOC,∠COE= ∠BOC和∠AOB=180°,求出即可;
∠BOC和∠AOB=180°,求出即可;
(3)根据∠COD= ∠AOC,∠COE=
∠AOC,∠COE= ∠BOC和∠AOB=α,求出即可.
∠BOC和∠AOB=α,求出即可.
点评:本题考查了角平分线定义的应用,主要考查学生能否熟练地运用角平分线定义进行计算,此题比较典型,难度也不大.
理由是:∵OD平分∠AOC,OE平分∠BOC,
∴∠COD=
 ∠AOC,∠COE=
∠AOC,∠COE= ∠BOC,
∠BOC,∵∠AOC>∠BOC,
∴∠COD>∠COE;
(2)解:能求出∠DOE的度数,是90°,
理由是:∠DOE=
 (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ∠AOB=
∠AOB= ×180°=90°.
×180°=90°.(3)解:能,∠DOE=
 α,
α,理由是:∵∠AOB=∠AOC+∠BOC=α,
∵OD平分∠AOC,OE平分∠BOC,
∴∠COD=
 ∠AOC,∠COE=
∠AOC,∠COE= ∠BOC,
∠BOC,∴∠DOE=
 ∠AOB=
∠AOB= α.
α.分析:(1)根据角平分线性质推出∠COD=
 ∠AOC,∠COE=
∠AOC,∠COE= ∠BOC,再根据已知求出即可;
∠BOC,再根据已知求出即可;(2)根据∠COD=
 ∠AOC,∠COE=
∠AOC,∠COE= ∠BOC和∠AOB=180°,求出即可;
∠BOC和∠AOB=180°,求出即可;(3)根据∠COD=
 ∠AOC,∠COE=
∠AOC,∠COE= ∠BOC和∠AOB=α,求出即可.
∠BOC和∠AOB=α,求出即可.点评:本题考查了角平分线定义的应用,主要考查学生能否熟练地运用角平分线定义进行计算,此题比较典型,难度也不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目