Question

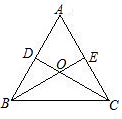如图，等边△ABC中，点D、E分别是边AB、AC的中点，CD、BE交于点O，则∠BOC的度数是________度．

Answer 1

120
分析：根据等边三角形的性质，确定CD、BE既为等边三角形的中线，又是三角形的高，然后根据四边形的内角和是360度解出∠DOE的度数，根据对顶角相等即可得出∠BOC的度数．
解答：∵△ABC为等边三角形，点D、E分别是边AB、AC的中点；
∴∠ADC=∠BEA=90°；
∵在四边形ADOE中，∠A=60°，∠ADC=∠BEA=90°；
∴∠DOE=360°-60°-90°-90°=120°；
∵对顶角相等；
∴∠BOC=120°．
故应填120°．
点评：此题考查了等边三角形的性质；解题的关键是∠ADC=∠BEA=90°是正确解答本题的关键．