题目内容
【题目】已知MN∥EF∥BC,点A、D为直线MN上的两动点,AD=a,BC=b,AE∶ED=m∶n;
(1)当点A、D重合,即a=0时(如图1),试求EF.(用含m,n,b的代数式表示)
(2)请直接应用(1)的结论解决下面问题:当A、D不重合,即a≠0,
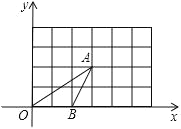
①如图2这种情况时,试求EF.(用含a,b,m,n的代数式表示)
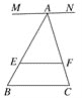
图1
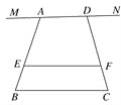
图2
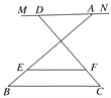
图3
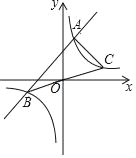
②如图3这种情况时,试猜想EF与a、b之间有何种数量关系?并证明你的猜想.
【答案】(1)EF=![]() ;(2)①EF=
;(2)①EF=![]() ;②猜想:EF=
;②猜想:EF=![]() ,证明详见解析.
,证明详见解析.
【解析】
(1)由EF∥BC,即可证得△AEF∽△ABC,根据相似三角形的对应边成比例,即可证得![]() =
=![]() ,根据比例变形,即可求得EF的值;
,根据比例变形,即可求得EF的值;
(2)①连接BD,与EF交于点H,由(1)知, HF=![]() ,EH=
,EH=![]() ,又由EF=EH+HF,即可求得EF的值;
,又由EF=EH+HF,即可求得EF的值;
②连接DE,并延长DE交BC于G,根据平行线分线段成比例定理,即可求得BG的长,又由EF=![]() 与GC=BC-BG,即可求得EF的值.
与GC=BC-BG,即可求得EF的值.
解 (1)∵EF∥BC,
∴△AEF∽△ABC,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
又BC=b,
∴![]() =
=![]() ,
,
∴EF=![]() ;
;
(2)①如图2,连接BD,与EF交于点H,
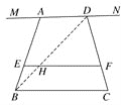
由(1)知,HF=![]() ,EH=
,EH=![]() ,
,
∵EF=EH+HF,
∴EF=![]() ;
;
②猜想:EF=![]() ,
,
证明:连接DE,并延长DE交BC于G,
由已知,得BG=![]() ,
,
EF=![]() ,
,
∵GC=BC-BG,
∴EF=![]() (BC-BG)=
(BC-BG)=![]() =
=![]() .
.

练习册系列答案
相关题目