Question

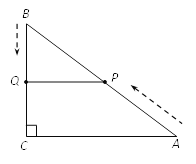
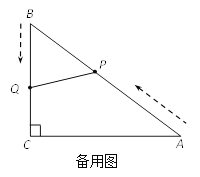
【题目】如图，在△ABC中，∠C=90°，AC=8cm，BC=6cm. 点P从点A出发，沿AB边以2 cm/s的速度向点B匀速移动；点Q从点B出发，沿BC边以1 cm/s的速度向点C匀速移动， 当一个运动点到达终点时，另一个运动点也随之停止运动，设运动的时间为t(s).

（1）当PQ∥AC时，求t的值；

（2）当t为何值时，△PBQ的面积等于cm 2.

Answer 1

【答案】（1）t=；（2）当t为2s或3s时，△PBQ的面积等于cm 2.

【解析】

（1）根据PQ∥AC得到△PBQ∽△ABC，列出比例式即可求解；

（2）解法一：过点Q作QE⊥AB于E，利用△BQE∽△BCA，得到，得到QE=t，根据S△PBQ =BP·QE=列出方程即可求解；

解法二：过点P作PE⊥BC于E，则PE∥AC，得到△BPE∽△BAC，则，求出PE=(10-2t).，利用S△PBQ =BQ·PE=列出方程即可求解.

（1）由题意得，BQ= tcm，AP=2 cm，则BP=（10—2t）cm

在Rt△ABC中，∠C=90°，AC=8cm，BC=6cm

∵ PQ∥AC， ∴ △PBQ∽△ABC，

∴ ，即 ，

解得 t=.

（2）解法一:

如图3，过点Q作QE⊥AB于E，则∠QEB =∠C=90°.

∵ ∠B =∠B,∴ △BQE∽△BCA，

∴ ，即 ， 解得 QE=t.

∴ S△PBQ =BP·QE=， 即·(10-2t)·t =.

整理，得t2-5t+6=0. 解这个方程，得t1=2，t2=3.

∵ 0＜t＜5，∴ 当t为2s或3s时，△PBQ的面积等于cm 2.

解法二：过点P作PE⊥BC于E，则PE∥AC（如图4）.

∵ PE∥AC.

∴ △BPE∽△BAC，

∴ ，即 ， 解得 PE=(10-2t).

∴ S△PBQ =BQ·PE=， 即·t·(10-2t)=

整理，得t2-5t+6=0. 解这个方程，得t1=2，t2=3.

∵ 0＜t＜5，

∴ 当t为2s或3s时，△PBQ的面积等于cm 2.