题目内容
 如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,则线段CN的长度为
如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A落在点F处,折痕为MN,则线段CN的长度为分析:根据折叠的性质,只要求出DN就可以求出NE,在直角△CEN中,若设CN=x,则DN=NE=8-x,CE=4cm,根据勾股定理就可以列出方程,从而解出CN的长.
解答:解:由题意设CN=x cm,则EN=(8-x)cm,
又∵CE=
DC=4cm,
∴在Rt△ECN中,EN2=EC2+CN2,即(8-x)2=42+x2,
解得:x=3,即CN=3cm.
故答案为:3cm.
又∵CE=
| 1 |
| 2 |
∴在Rt△ECN中,EN2=EC2+CN2,即(8-x)2=42+x2,
解得:x=3,即CN=3cm.
故答案为:3cm.
点评:本题考查翻折变换的问题,折叠问题其实质是轴对称,对应线段相等,对应角相等,找到相应的直角三角形利用勾股定理求解是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
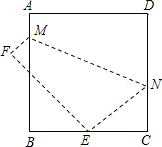 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN长是( )
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN长是( )| A、3cm | B、4cm | C、5cm | D、6cm |
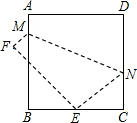 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则折痕MN的长是( )
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则折痕MN的长是( )A、4
| ||
B、4
| ||
C、4
| ||
D、4
|
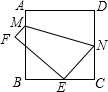 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN的长是
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN的长是 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,求线段CN长.
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,求线段CN长.