题目内容
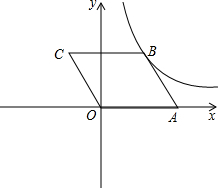 (2012•长春)如图,在平面直角坐标系中,?OABC的顶点A、C的坐标分别为A(2,0)、C(-1,2),反比例函数y=
(2012•长春)如图,在平面直角坐标系中,?OABC的顶点A、C的坐标分别为A(2,0)、C(-1,2),反比例函数y=| k |
| x |
(1)求k的值.
(2)将?OABC沿x轴翻折,点C落在点C′处,判断点C′是否在反比例函数y=
| k |
| x |
分析:(1)根据平行四边形的性质可得AO=BC,再根据A、C点坐标可以算出B点坐标,再把B点坐标代入反比例函数解析式中即可求出k的值;
(2)根据翻折方法可知C与C′点关于x轴对称,故C′点坐标是(-1,-2),把C′点坐标(-1,-2)代入解析式发现能使解析式左右相等,故点C′是否在反比例函数y=
的图象上.
(2)根据翻折方法可知C与C′点关于x轴对称,故C′点坐标是(-1,-2),把C′点坐标(-1,-2)代入解析式发现能使解析式左右相等,故点C′是否在反比例函数y=
| 2 |
| x |
解答: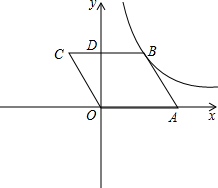 解:(1)∵四边形OABC是平行四边形,
解:(1)∵四边形OABC是平行四边形,
∴BC=AO,
∵A(2,0),
∴OA=2,
∴BC=2,
∵C(-1,2),
∴CD=1,
∴BD=BC-CD=2-1=1,
∴B(1,2),
∵反比例函数y=
(k≠0)的图象经过点B,
∴k=1×2=2;
(2)∵?OABC沿x轴翻折,点C落在点C′处,
∴C′点坐标是(-1,-2),
∵k=2,
∴反比例函数解析式为y=
,
把C′点坐标(-1,-2)代入函数解析式能使解析式左右相等,
故点C′在反比例函数y=
的图象上.
 解:(1)∵四边形OABC是平行四边形,
解:(1)∵四边形OABC是平行四边形,∴BC=AO,
∵A(2,0),
∴OA=2,
∴BC=2,
∵C(-1,2),
∴CD=1,
∴BD=BC-CD=2-1=1,
∴B(1,2),
∵反比例函数y=
| k |
| x |
∴k=1×2=2;
(2)∵?OABC沿x轴翻折,点C落在点C′处,
∴C′点坐标是(-1,-2),
∵k=2,
∴反比例函数解析式为y=
| 2 |
| x |
把C′点坐标(-1,-2)代入函数解析式能使解析式左右相等,
故点C′在反比例函数y=
| 2 |
| x |
点评:此题主要考查了反比例函数点的坐标与反比例函数解析式的关系,以及平行四边形的性质,关键是熟练把握凡是反比例函数图象经过的点都能满足解析式.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
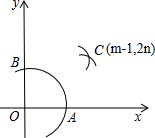 (2012•长春)如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于
(2012•长春)如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于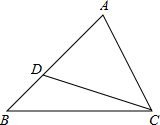 (2012•长春)如图,在△ABC中,AB=5,AC=4,点D在边AB上,∠ACD=∠B,则AD的长为
(2012•长春)如图,在△ABC中,AB=5,AC=4,点D在边AB上,∠ACD=∠B,则AD的长为 (2012•长春)如图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查,结果为(单位:人):30,31,27,26,31.这组数据的中位数是( )
(2012•长春)如图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查,结果为(单位:人):30,31,27,26,31.这组数据的中位数是( )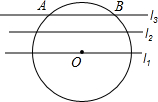 (2012•长春)如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.
(2012•长春)如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.