题目内容
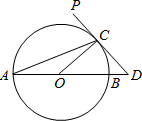13、如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于D，且CO=CD，则∠PCA=（ ）分析：根据图形利用切线的性质，得到∠COD=45°，连接AC，∠ACO=22.5°，所以∠PCA=90°-22.5°=67.5°．
解答：解：如图：∵PD切⊙O于点C，
∴OC⊥PD，
又∵OC=CD，
∴∠COD=45°，
∵AO=CO，
∴∠ACO=22.5°，
∴∠PCA=90°-22.5°=67.5°．
故选D．
∴OC⊥PD，
又∵OC=CD，
∴∠COD=45°，
∵AO=CO，
∴∠ACO=22.5°，
∴∠PCA=90°-22.5°=67.5°．
故选D．
点评：本题考查的是切线的性质，利用切线的性质得到OC⊥PD，然后进行计算求出∠PCA的度数．
练习册系列答案
相关题目
如图，已知⊙O的直AB=20cm，CD垂AB于E，CD=12cm，AE的长为（ ）| A、1cm | B、2cm | C、3cm | D、4cm |
如图，在水塔O的东北方向32m处有一抽水站A，在水塔的东南方向24m处有一建筑工地B，在AB间建一条直水管，则水管的长为
如图，已知⊙O的直AB=20cm，CD垂AB于E，CD=12cm，AE的长为