题目内容
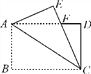
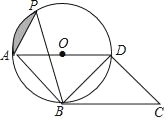
【题目】如图,△PAB内接于⊙O,ABCD的边AD是⊙O的直径,且∠C=∠APB,连接BD.
(1)求证:BC是⊙O的切线.
(2)若BC=2,∠PBD=60°,求![]() 与弦AP围成的阴影部分的面积.
与弦AP围成的阴影部分的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接OB,利用平行四边形的性质,切线的判定定理即可得到BC是⊙O的切线;
(2)连结OP,作OE⊥AP于E,在Rt△OAE中中,利用三角函数得到OE,然后根据扇形面积公式进行计算即可.
解:(1)连结OB,
∵四边形ABCD是平行四边形,
∴∠C=∠BAD,AD∥BC,
∵∠APB=∠ADB,∠C=∠APB,
∴∠BAD=∠ADB,
∴AB=BD,
∵OA=OD,
∴OB⊥AD,
∴∠AOB=90°,
∵AD∥BC,
∴∠OBC=∠AOB=90°,
∴OB⊥BC,
∵OB为半径,
∴BC是⊙O的切线.
(2)连结OP,作OE⊥AP于E,
∵∠PAD=∠PBD=60°,OA=OP,
∴PA=OA=OP,∠AOP=60°,
在ABCD中,AD=BC=2,
∴AP=OA=1,
在Rt△OAE中,OE=OAsin60°=![]() ,
,
![]() 与弦AP围成的阴影部分的面积为:
与弦AP围成的阴影部分的面积为:![]() ﹣
﹣![]() ×1×
×1×![]() =
=![]() ﹣
﹣![]() .
.

【题目】物理兴趣小组![]() 位同学在实验操作中的得分情况如下表:
位同学在实验操作中的得分情况如下表:
得分(分) |
|
|
|
|
人数(人) |
|
|
|
|
问:(1)这![]() 位同学实验操作得分的众数是 ,中位数是
位同学实验操作得分的众数是 ,中位数是
(2)这![]() 位同学实验操作得分的平均分是多少?
位同学实验操作得分的平均分是多少?
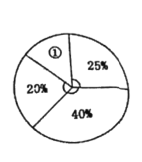
(3)将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?
【题目】某市现在有两种用电收费方法:
分时电表 | 普通电表 | |
峰时(8:00~21:00) | 谷时(21:00到次日8:00) | |
电价0.55元/千瓦·时 | 电价0.35元/千瓦·时 | 电价0.52元/千瓦·时 |
小明家所在的小区用的电表都换成了分时电表.
解决问题:
(1)小明家庭某月用电总量为![]() 千瓦·时(
千瓦·时(![]() 为常数);谷时用电
为常数);谷时用电![]() 千瓦·时,峰时用电
千瓦·时,峰时用电![]() 千瓦·时,分时计价时总价为
千瓦·时,分时计价时总价为![]() 元,普通计价时总价为
元,普通计价时总价为![]() 元,求
元,求![]() ,
,![]() 与用电量的函数关系式.
与用电量的函数关系式.
(2)小明家庭使用分时电表是不是一定比普通电表合算呢?
(3)下表是路皓家最近两个月用电的收据:
谷时用电(千瓦·时) | 峰时用电(千瓦·时) |
181 | 239 |
根据上表,请问用分时电表是否合算?