题目内容
【题目】如图，在矩形ABCD中，点A为坐标原点，点B在x轴正半轴，点D在y轴正半轴，点C坐标为（6，m），点E是CD的中点，以CE为一边在矩形ABCD的内部作矩形CEFG，使点F在直线y=x上，交线段BC于点G，直线DG的函数表达式为y=- 
x+4，直线DG和AF交于点H．
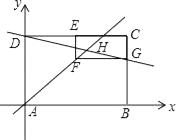
（1）求m的值；
（2）求点H的坐标；
（3）判断直线BE是否经过点H，并说明理由．
【答案】
（1）解：∵直线DG的函数表达式为y=﹣ 
x+4，
∴D（0，4），
∵四边形ABCD是矩形，且C（6，m），
∴m=4，
∴C（6，4）
（2）解：∵直线AF：y=x与直线DG：y=﹣ x+4的交点为H，
∴ 
，
∴ 
，
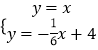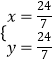∴H（ 
， ）
（3）解：直线BE过点H，
理由：
∵直线DG解析式为y=﹣ x+4，直线BC解析式为x=6，
∴G（6，3），
∴点F的纵坐标为3，
∵点F在直线AF上，
∴F点的横坐标为3，
∴F（3，3），
∴点E的横坐标为3，
∵直线DC解析式为y=4，
∴E（3，4），
∵B（6，0），
∴直线BE解析式为y=﹣ 
x+8，
当x= 时，y=﹣ × +8= ，
∴直线BE过点H
【解析】（1） 根据直线DG的解析式求出其与y轴交点D的坐标，根据正方形的对边批平行性质，平行于x轴的直线上的点的纵坐标相同及C点的坐标求出m的值，从而得出答案；
（2）求直线AF：y=x与直线DG：y=﹣ x+4的交点H的坐标，即求两直线解析式组成的方程组的解；
（3）直线DG解析式与直线BC解析式求出G点的坐标，根据平行于x轴的直线纵坐标相等得出点F的纵坐标为3，又点F在直线AF上，故F点的横坐标为3，从而得出F点的坐标，又因E,F所在的直线平行于y轴，故点E的横坐标为3，又直线DC解析式为y=4，故E（3，4）用待定系数法求出直线BE解析式，根据一次函数图像上点的坐标特点判断即可。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法．
