题目内容
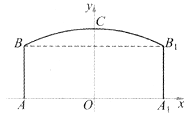
如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6 m.
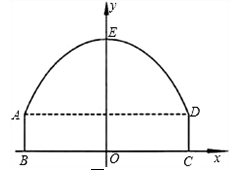
(1)求抛物线的解析式;
(2)如果该隧道内设双行道,现有一辆货运卡车高为4.2 m,宽为2.4 m,这辆货运卡车能否通过该隧道?通过计算说明.
(2)如果该隧道内设双行道,现有一辆货运卡车高为4.2 m,宽为2.4 m,这辆货运卡车能否通过该隧道?通过计算说明.
解:设抛物线的解析式为y=ax2+6,又因为抛物线过点(4,2),则16a+6=2,

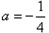 ,
,
 抛物线的解析式为y=
抛物线的解析式为y=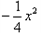 +6.
+6.
(2)当x=2.4时,y=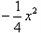 +6 =-1. 44+6=4. 56>4.2,
+6 =-1. 44+6=4. 56>4.2,
故这辆货运卡车能通过该隧道.

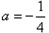 ,
,  抛物线的解析式为y=
抛物线的解析式为y=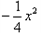 +6.
+6. (2)当x=2.4时,y=
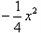 +6 =-1. 44+6=4. 56>4.2,
+6 =-1. 44+6=4. 56>4.2,故这辆货运卡车能通过该隧道.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 的距离为8m.
的距离为8m.