题目内容
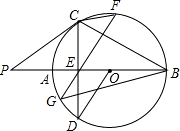 已知:如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆与G、F两点,连接CF、BG.则下列结论:
已知:如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆与G、F两点,连接CF、BG.则下列结论:
①CD⊥AB;②PC是⊙O的切线;③OD∥GF;④弦CF的弦心距等于 BG.则其中正确的是
BG.则其中正确的是
- A.①②④
- B.③④
- C.①②③
- D.①②③④
A
分析:连接BD、OC、AG,过O作OQ⊥CF于Q,OZ⊥BG于Z,求出∠ABC=∠ABD,求出弧AC=弧AD,根据垂径定理求出即可;求出∠P+∠PCD=90°和∠P=∠DCO即可求出PC是圆的切线;采用反证法求出∠B=30°,但已知没有给出此条件,即可判断③;求出CF=AG,推出CQ=OZ,证△OCQ≌△BOZ,推出OQ=BZ,即可判断④.
解答: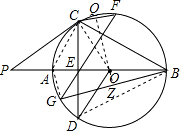 连接BD、OC、AG,过O作OQ⊥CF于Q,OZ⊥BG于Z,
连接BD、OC、AG,过O作OQ⊥CF于Q,OZ⊥BG于Z,
∵OD=OB,
∴∠ABD=∠ODB,
∵∠AOD=∠OBD+∠ODB=2∠OBD,
∵∠AOD=2∠ABC,
∴∠ABC=∠ABD,
∴弧AC=弧AD,
∵AB是直径,
∴CD⊥AB,
∴①正确;
∵CD⊥AB,
∴∠P+∠PCD=90°,
∵OD=OC,
∴∠OCD=∠ODC=∠P,
∴∠PCD+∠OCD=90°,
∴∠PCO=90°,
∴PC是切线,∴②正确;
假设OD∥GF,则∠AOD=∠FEB=2∠ABC,
∴3∠ABC=90°,
∴∠ABC=30°,
已知没有给出∠B=30°,∴③错误;
∵AB是直径,
∴∠ACB=90°,
∵EF⊥BC,
∴AC∥EF,
∴弧CF=弧AG,
∴AG=CF,
∵OQ⊥CF,OZ⊥BG,
∴CQ= AG,OZ=
AG,OZ= AG,BZ=
AG,BZ= BG,
BG,
∴OZ=CQ,
∵OC=OB,∠OQC=∠OZB=90°,
∴△OCQ≌△BOZ,
∴OQ=BZ= BG,
BG,
∴④正确.
故选A.
点评:本题考查了切线的判定、全等三角形的性质和判定、圆周角定理、垂径定理等知识点的运用,主要考查学生运用定理进行推理的能力,题目比较好,但有一定的难度.
分析:连接BD、OC、AG,过O作OQ⊥CF于Q,OZ⊥BG于Z,求出∠ABC=∠ABD,求出弧AC=弧AD,根据垂径定理求出即可;求出∠P+∠PCD=90°和∠P=∠DCO即可求出PC是圆的切线;采用反证法求出∠B=30°,但已知没有给出此条件,即可判断③;求出CF=AG,推出CQ=OZ,证△OCQ≌△BOZ,推出OQ=BZ,即可判断④.
解答:
 连接BD、OC、AG,过O作OQ⊥CF于Q,OZ⊥BG于Z,
连接BD、OC、AG,过O作OQ⊥CF于Q,OZ⊥BG于Z,∵OD=OB,
∴∠ABD=∠ODB,
∵∠AOD=∠OBD+∠ODB=2∠OBD,
∵∠AOD=2∠ABC,
∴∠ABC=∠ABD,
∴弧AC=弧AD,
∵AB是直径,
∴CD⊥AB,
∴①正确;
∵CD⊥AB,
∴∠P+∠PCD=90°,
∵OD=OC,
∴∠OCD=∠ODC=∠P,
∴∠PCD+∠OCD=90°,
∴∠PCO=90°,
∴PC是切线,∴②正确;
假设OD∥GF,则∠AOD=∠FEB=2∠ABC,
∴3∠ABC=90°,
∴∠ABC=30°,
已知没有给出∠B=30°,∴③错误;
∵AB是直径,
∴∠ACB=90°,
∵EF⊥BC,
∴AC∥EF,
∴弧CF=弧AG,
∴AG=CF,
∵OQ⊥CF,OZ⊥BG,
∴CQ=
 AG,OZ=
AG,OZ= AG,BZ=
AG,BZ= BG,
BG,∴OZ=CQ,
∵OC=OB,∠OQC=∠OZB=90°,
∴△OCQ≌△BOZ,
∴OQ=BZ=
 BG,
BG,∴④正确.
故选A.
点评:本题考查了切线的判定、全等三角形的性质和判定、圆周角定理、垂径定理等知识点的运用,主要考查学生运用定理进行推理的能力,题目比较好,但有一定的难度.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 22、已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.
22、已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC. (2013•门头沟区一模)已知:如图,AB是⊙O的直径,AC是⊙O的弦,M为AB上一点,过点M作DM⊥AB,交弦AC于点E,交⊙O于点F,且DC=DE.
(2013•门头沟区一模)已知:如图,AB是⊙O的直径,AC是⊙O的弦,M为AB上一点,过点M作DM⊥AB,交弦AC于点E,交⊙O于点F,且DC=DE.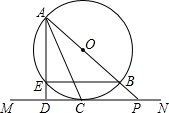 (1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP.
(1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP.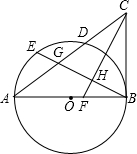 (2012•平谷区二模)已知,如图,AB是⊙O的直径,点E是
(2012•平谷区二模)已知,如图,AB是⊙O的直径,点E是
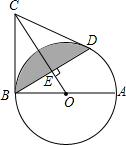 已知:如图,AB是⊙O的直径,BC为⊙O的切线,过点B的弦BD⊥OC交⊙O于点D,垂足为E.
已知:如图,AB是⊙O的直径,BC为⊙O的切线,过点B的弦BD⊥OC交⊙O于点D,垂足为E.