题目内容
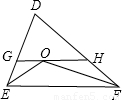
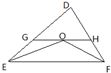 15、如图,△DEF中,∠DEF、∠DFE的平分线相于点O,直线GH过点O与EF平行,分别与DE、DF交于点G、H.且DE=8,DF=7,则△DGH的周长=
15、如图,△DEF中,∠DEF、∠DFE的平分线相于点O,直线GH过点O与EF平行,分别与DE、DF交于点G、H.且DE=8,DF=7,则△DGH的周长=15.
.分析:根据角平分线的定义以及平行的性质,可知∠GEO=∠GOE,∠HOF=∠HFO,得出GE=GO,OH=HF,即可得出△DGH的周长=DG+GO+DH+HO,根据等量代换可知△DGH的周长=DE+DF=15.
解答:解:∵EO,FO分别为∠DEF,∠DFE的角平分线,
∴∠GEO=∠OEF,∠HFO=∠OFE,
∵GH∥EF,
∴∠GOE=∠OEF,∠HOF=∠OFE,
∴∠GEO=∠GOE,∠HOF=∠HFO,
∴GE=GO,OH=HF,
∴△DGH的周长=DG+GO+DH+HO=DE+DF=15.
故答案为:15.
∴∠GEO=∠OEF,∠HFO=∠OFE,
∵GH∥EF,
∴∠GOE=∠OEF,∠HOF=∠OFE,
∴∠GEO=∠GOE,∠HOF=∠HFO,
∴GE=GO,OH=HF,
∴△DGH的周长=DG+GO+DH+HO=DE+DF=15.
故答案为:15.
点评:本题考查了角平分线的定义以及平行的性质,根据等量代换得出△DGH的周长即为DE与DF的和,难度适中.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
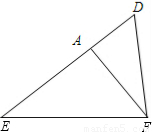
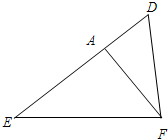 23、如图,△DEF中,∠EDF=2∠E,FA⊥DE于点A,问:DF、AD、AE间有什么样的三边大小关系?
23、如图,△DEF中,∠EDF=2∠E,FA⊥DE于点A,问:DF、AD、AE间有什么样的三边大小关系?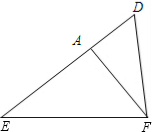 如图,△DEF中,∠EDF=2∠E,FA⊥DE于点A,问:DF、AD、AE间有什么样的三边大小关系?
如图,△DEF中,∠EDF=2∠E,FA⊥DE于点A,问:DF、AD、AE间有什么样的三边大小关系?