题目内容
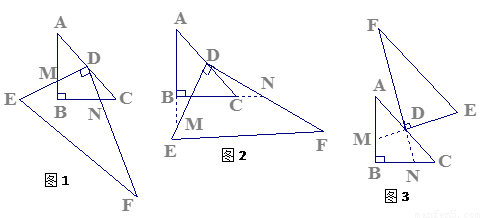
如图1,已知△ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的△DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转。
⑴在图1中,DE交AB于M,DF交BC于N。①说明DM=DN;②在这一过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;
⑵继续旋转至如图2的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立,请给出理由;若不成立,请说明理由;
⑶继续旋转至如图3的位置,延长FD交BC于N,延长ED交AB于M,DM=DN是否仍然成立?若成立,请给出结论,不用说明理由。
解:(1)①连接BD,∵AB=BC,∠ABC=90,∴△ABC是等腰直角三角形,
∴∠A=∠C=45 ∵D是AC的中点,∴BD是△ABC的中线,∴BD是△ABC的高,
∴∠BDC=90,∴∠DBC=45=∠DCB,∴BD=CD=AD,∴∠DBC=∠DAB=45,
∵∠EDF=90=∠ADB,∠EDB为公共角,∴∠ADM=∠BDN,∴△ADM≌△BDN(ASA),
∴DM=DN.
②四边形DMBN的面积不发生变化,理由如下:
由①可知S△ADM=S△BDN,∴S四边形DMBN=S△ADB,已知△ADB的面积是一个定值
∴四边形DMBN的面积不发生变化,∵AB=AC=1,S△ADB=1/2S△ABC,
∴S四边形DMBN=S△ABD=1/2S△ABC=1/4.
(2)连接BD,由(1)可知,BD=CD,∵FDE=90,∴∠FDN=90,
∵∠BDC=90,∠FDC是公共角,∴∠BDM=∠CDN,∵∠MBE=∠NDE,
∠BEM=∠NED,∴∠M=∠N,∴△BMD≌△CND(AAS)
∴DM=DN
(3)DM=DN
【解析】(1)连结BD,证明△BDM与△CDN全等,得DM=DN
(2)连结BD,同理可证△BDM与△CDN全等,得DM=DN
(3)结论成立 DM=DN

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案 定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.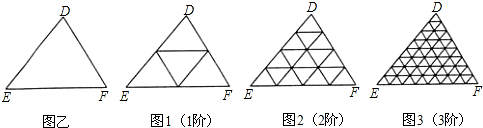
 如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=
如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=

