题目内容
【题目】(本题14分)已知,在矩形ABCD中,AB=6,BC=8,将矩形ABCD绕着点D按着顺时针方向旋转![]() 得到矩形A/B/C/D,直线DA/、B/C/分别与直线BC相交于点P、Q.
得到矩形A/B/C/D,直线DA/、B/C/分别与直线BC相交于点P、Q.
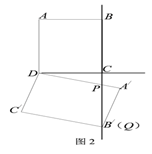
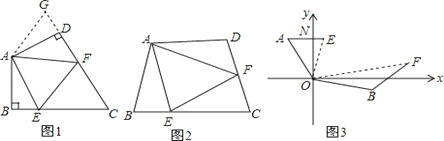
(1)如图1,当矩形A/B/C/D的顶点B/落在射线DC上时,PC的长为_________;
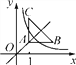
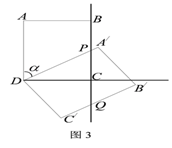
如图2,当矩形A/B/C/D的顶点B/落在射线BC上时,PC的长为_________;
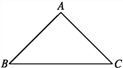
(2)①如图3,当点P位于线段BC上时,求证:DP=PQ.
②在矩形ABCD旋转的过程中(旋转角![]() 满足
满足![]() ),试求出当
),试求出当![]() 时PC的长.
时PC的长.
(3)在矩形ABCD旋转的过程中(旋转角![]() 满足
满足![]() ),以D,B/,P,Q为顶点的四边形能否成为平行四边形?若能,直接写出此时PC的长(或PC的取值范围);若不能,请简要说明理由.
),以D,B/,P,Q为顶点的四边形能否成为平行四边形?若能,直接写出此时PC的长(或PC的取值范围);若不能,请简要说明理由.
【答案】 (1)![]() ;.
;. ![]() ,(2)①证明方法较多.如连结DQ,先证△DCQ≌△DC/Q,再证∠PDQ=∠PQD.等等.②CP=9+
,(2)①证明方法较多.如连结DQ,先证△DCQ≌△DC/Q,再证∠PDQ=∠PQD.等等.②CP=9+![]() 或
或![]() (3)CP=8
(3)CP=8
【解析】:(1)①根据相似三角形的性质得出边的比值即可; ②由全等三角形的判定和性质得出边的关系,再根据勾股定理得出方程解答即可; (2)①由矩形的性质得出线段相等,再利用全等三角形进行判断,利用其性质证明即可; ②根据全等三角形判定和性质得出线段关系,再利用勾股定理得出方程解答即可;
(3)分几种情况进行分析得出以点D,B′,P,Q为顶点的四边形能否成为平行四边形,进而得出CP的值.
解:(1)①∵将矩形ABCD绕点D按顺时针方向旋转,得到矩形A′B′C′D′,AB=6,BC=8,
∴△CDP∽△A′DB′
∴CP=![]() ,
,
同理可得,CP=![]() .
.
(2)①如图所示.
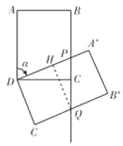
过点Q作QH⊥DA′于H,
则∠QHD=∠HDC′=∠C′=90°,
∴四边形QHDC′为矩形,
∴QH=DC′=DC,
在△DCP和△QHP中,
∵∠QHP=∠DCP=90°×∠QPH=∠DPC×QH=DC,
∴△DCP≌△QHP,
∴DP=PQ.
②当点P在线段BC上时,如图所示,
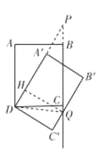
则DP=BP=x,PC=8-x,
在Rt△PCD中,(8-x)2+62=x2,解得x=![]() ,
,
∴PC=BC-BP=8-![]() =
=![]() ,
,
∴矩形ABCD旋转(当0°< ![]() ≤90°时)过程中.
≤90°时)过程中.
当BP=![]() BQ时,CP的长是9+
BQ时,CP的长是9+![]()
![]() 或
或![]() .
.
(3)CP=8.
解法:设矩形DA′B′C′的对角线与直线BC的交点为S.
①当B/在直线BC的右侧时,虽然DP∥B′Q,
但总有DS≥DC>![]() DB′=5,即PQ与B′Q不互相平分,
DB′=5,即PQ与B′Q不互相平分,
以D、B′、P、Q为顶点不能构成平行四边形;
②当B/在直线BC上时,B′、P、Q三点在一条直线上,所以,以D、B′、P、Q为顶点不能构成平行四边形;
③当 B′落在线段AD的延长线上时,如图所示,
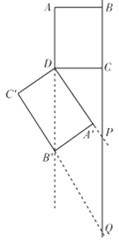
DP∥B′Q,且DB′∥PQ,所以四边形DB′QP为平行四边形,
此时△PCD≌△DA′B,CP=DA′=8;
④当B′在直线BC与直线AD所夹区域时,虽然DP∥B′Q,但DB′与PQ不平行,
所以,以D、B′、P、Q为顶点不能构成平行四边形;
综上,只有B′落在线段AD的延长线上时,四边形DB/QP为平行四边形,此时CP=8.
“点睛”本题考查了矩形的性质,旋转的性质,全等三角形的判定与性质,勾股定理的应用,找出两根三角形的高的关系是本题的关键.

 口算题天天练系列答案
口算题天天练系列答案【题目】老师计算学生的学期总评成绩按照如下的标准:平时作业占10%,单元测验占30%,期中考试占25%,期末考试占35%.小丽和小明的成绩如下所示:
学生 | 平时作业 | 单元测验 | 期中考试 | 期未考试 |
小丽 | 80 | 75 | 71 | 88 |
小明 | 76 | 80 | 70 | 90 |
请你通过计算,比较谁的学期总评成绩高?