题目内容
【题目】在平面直角坐标系中,抛物线y=![]() 交x轴于点A、B(点A在点B的左侧),交y轴于点C.
交x轴于点A、B(点A在点B的左侧),交y轴于点C.
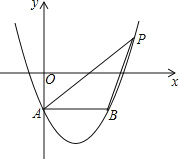
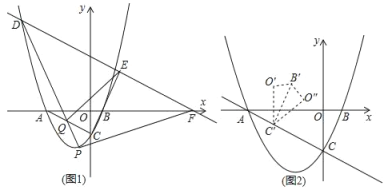
(1)如图,点D是抛物线在第二象限内的一点,且满足|xD﹣xA|=2![]() ,过点D作AC的平行线,分别与x轴、射线CB交于点F、E,点P为直线AC下方抛物线上的一动点,连接PD交线段AC于点Q,当四边形PQEF的面积最大时,在y轴上找一点M,x轴上找一点N,使得PM+MN﹣
,过点D作AC的平行线,分别与x轴、射线CB交于点F、E,点P为直线AC下方抛物线上的一动点,连接PD交线段AC于点Q,当四边形PQEF的面积最大时,在y轴上找一点M,x轴上找一点N,使得PM+MN﹣![]() NB取得最小值,求这个最小值;
NB取得最小值,求这个最小值;
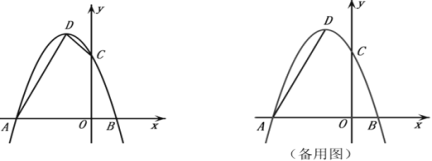
(2)如图2,将△BOC沿着直线AC平移得到△B′O′C′,再将△B'O′C′沿B′C′翻折得到△B′O″C′,连接BC′、O″B,则△C′BO″能否构成等腰三角形?若能,请直接写出所有符合条件的点O″的坐标,若不能,请说明理由.
【答案】(1)P′W=3![]() ;(2)点O″的坐标为(﹣
;(2)点O″的坐标为(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
1)根据|xD﹣xA|=2![]() ,求出点D的坐标,转换四边形PQEF的面积最大即为线段PH最大,PM+MN﹣
,求出点D的坐标,转换四边形PQEF的面积最大即为线段PH最大,PM+MN﹣![]() NB取得最小值,将这三条线段转化为共线即可.
NB取得最小值,将这三条线段转化为共线即可.
(2)设点O′、B′、C′的坐标,求出点O″的坐标,利用两点间距离公式表示线段长度,分三种情况讨论即可.
(1)令![]() =0,
=0,
解得x1=![]() ,x2=﹣4
,x2=﹣4![]() ,
,
∴A(﹣4![]() ,0),B(
,0),B(![]() ,0),
,0),
令x=0,y=﹣2![]() ,
,
∴C(0,﹣2![]() ),
),
∵|xD﹣xA|=2![]() ,点D是抛物线在第二象限内的一点,
,点D是抛物线在第二象限内的一点,
∴D的横坐标为﹣6![]() ,
,
∴D(﹣6![]() ,7
,7![]() ),
),
设直线BC的解析式为y=kx+b,
则有![]()
解得![]()
∴直线BC的解析式为y=2x﹣2![]() ,
,
设直线AC的解析式为y=k1x+b1,
则有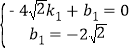
解得
∴直线AC的解析式为y=﹣![]() x﹣2
x﹣2![]() ,
,
∵DE∥AC,
∴设直线DE的解析式为y=﹣![]() x+b2,代入点D(﹣6
x+b2,代入点D(﹣6![]() ,7
,7![]() ),
),
解得b2=4![]() ,
,
∴直线DE的解析式为y=﹣![]() x+4
x+4![]() ,
,
令y=0,此时x=8![]() ,
,
∴F(8![]() ,0),
,0),
令2x﹣2![]() =﹣
=﹣![]() x+4
x+4![]() ,
,
解得x=![]() ,
,
∴E(![]() ,
,![]() ),
),
∵S四边形PQEF=S△PDF﹣S△PQE=S△PDF﹣S△DAE,
∵D、A、E是固定点,
∴S△DAE是固定值,即要使四边形PQEF的面积最大,只需△PDF的面积最大,
如图1所示,
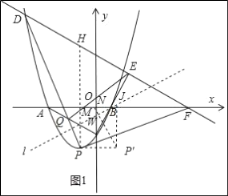
过点P作x轴的垂线交DF于点H,则S△PDF=![]() PH|xF﹣xD|=7
PH|xF﹣xD|=7![]() PH,
PH,
∴当PH最大时,S△PDF最大,
设点P的坐标为(a,![]() a2+
a2+![]() a﹣2
a﹣2![]() ),则点H为(a,﹣
),则点H为(a,﹣![]() a+4
a+4![]() ),
),
∴PH=﹣![]() a2﹣2a+6
a2﹣2a+6![]() =﹣
=﹣![]() (a+2
(a+2![]() )2+8
)2+8![]() ,
,
∴当a=﹣2![]() 时,PH最大,
时,PH最大,
此时P(﹣2![]() ,﹣3
,﹣3![]() ),
),
作点P关于y轴的对称点P′(2![]() ,﹣3
,﹣3![]() ),
),
过点B作直线l:y=![]() x﹣
x﹣![]() ,
,
过点P′作直线l的垂线交l于点W,交y轴于点M,交x轴于点N,
∴![]() NB=NW,
NB=NW,
∴PM+MN﹣![]() NB=PM+MN﹣NW=P′N﹣NW=P′W,
NB=PM+MN﹣NW=P′N﹣NW=P′W,
∴P′W即为所求,
过P′作y轴的平行线交l于点J,
则J(2![]() ,
,![]() ),
),
则JP′=![]() ,
,
则P′W=![]() JP′=3
JP′=3![]() .
.
(2)设△BOC在水平方向上移动了2![]() t个单位,则在竖直方向上移动了
t个单位,则在竖直方向上移动了![]() t个单位,
t个单位,
则C′(﹣2![]() t,﹣2
t,﹣2![]() t+
t+![]() t),O′(﹣2
t),O′(﹣2![]() t,
t,![]() t),
t),
如图2所示,过O″作y轴的平行线交O′B′的延长线于点M,
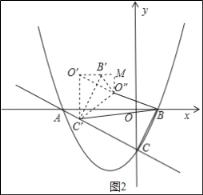
O′O″=2×![]() ×
×![]() =
=![]() ,
,
∴O″M=![]() ,O′M=
,O′M=![]() ,
,
∴O″(![]() ﹣2
﹣2![]() t,﹣
t,﹣![]() +
+![]() t),
t),
∴C′B=![]() =
=![]() ,
,
C′O″=2![]() ,
,
O″B=![]() =
=![]()
①![]() =2
=2![]() ,无解.
,无解.
②![]() =
=![]() ,解得t=-1,
,解得t=-1,
∴O″(﹣![]() ,
,![]() ),
),
③![]() =2
=2![]() ,解得t1=
,解得t1=![]() ,t2=
,t2=![]() ,
,
∴O″(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
综上所述:点O″的坐标为(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】某校开展“走进中国数学史”为主题的知识竞赛活动,八、九年级各有200名学生参加竞赛,为了解这两个年级参加竞赛学生的成绩情况,从中各随机抽取20名学生的成绩,数据如下:
八年级 | 91 | 89 | 77 | 86 | 71 | 九年级 | 84 | 93 | 66 | 69 | 76 |
51 | 97 | 93 | 72 | 91 | 87 | 77 | 82 | 85 | 88 | ||
81 | 92 | 85 | 85 | 95 | 90 | 88 | 67 | 88 | 91 | ||
88 | 88 | 90 | 64 | 91 | 96 | 68 | 97 | 99 | 88 |
整理上面数据,得到如下统计表:
成绩 人数 年级 |
|
|
|
|
|
八年级 | 1 | 1 | 3 | 7 | 8 |
九年级 | 0 | 4 | 2 | 8 | 6 |
样本数据的平均数、中位数、众数、方差如下表所示:
统计表 年级 | 平均数 | 中位数 | 众数 | 方差 |
八年级 | 83.85 | 88 | 91 | 127.03 |
九年级 | 83.95 | 87.5 | | 99.45 |
根据以上信息,回答下列问题:
(1)写出上表中众数![]() 的值.
的值.
(2)试估计八、九年级这次选拔成绩80分以上的人数和.
(3)你认为哪个年级学生的竞赛成绩较好?说明你的理由.(至少从两个不同的角度说明推断的合理性)