题目内容
【题目】把正整数1,2,3,4,…,2017排列成如下图所示的一个数表: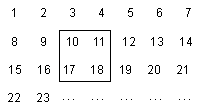
(1)用一正方形在表中随意框住4个数,把其中最小的数记为 ![]() ,另三个数用含
,另三个数用含 ![]() 的式子表示出来,从大到小依次是 , , ;
的式子表示出来,从大到小依次是 , , ;
(2)当被框住的4个数之和等于416时, ![]() 的值是多少?
的值是多少?
(3)被框住的4个数之和能否等于622?如果能,请求出此时 ![]() 的值;如果不能,请说明理由.
的值;如果不能,请说明理由.
【答案】
(1)x+1;x+7;x+8
(2)解:x+(x+1)+(x+7)+(x+8)=416,4x+16=416,x=100
(3)解:被框住的4个数之和不可能等于622x+(x+1)+(x+7)+(x+8)=622,4x+16=622,x=151.5,∵x是正整数,不可能是151.5,∴被框住的4个数之和不可能等于622
【解析】解:(1)从表格可看出框的4个数,左右相邻的差1,上下相邻的差7,设最小的数是x , 右边的就为x+1,x下面的就为x+7,x+7右边的为x+8,所以这三个数为x+1,x+7,x+8;(1)从表格可看出框的4个数,左右相邻的差1,上下相邻的差7,列出代数式;(2)由被框住的4个数之和等于416,列出方程,求出方程的解;(3)根据题列出方程,求出x的值,由x是正整数,不是小数,得到被框住的4个数之和不可能等于622.

练习册系列答案
相关题目