题目内容
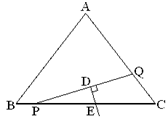
如图13,在等腰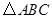 中,
中,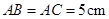 ,
,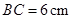 ,点
,点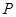 从点
从点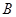 开始沿
开始沿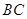 边以每秒1
边以每秒1 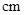 的速度向点
的速度向点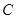 运动,点
运动,点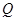 从点
从点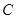 开始沿
开始沿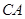 边以每秒2
边以每秒2 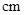 的速度向点
的速度向点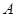 运动,
运动,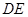 保持垂直平分
保持垂直平分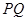 ,且交
,且交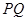 于点
于点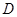 ,交
,交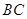 于点
于点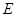 .点
.点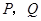 分别从
分别从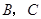 两点同时出发,当点
两点同时出发,当点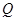 运动到点
运动到点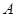 时,点
时,点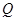 、
、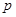 停止运动,设它们运动的时间为
停止运动,设它们运动的时间为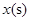 .
.
(1)当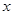 = 秒时,射线
= 秒时,射线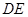 经过点
经过点 ;
;
(2)当点 运动时,设四边形
运动时,设四边形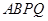 的面积为
的面积为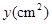 ,求
,求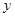 与
与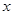 的函数关系式(不用写出自变量取值范围);
的函数关系式(不用写出自变量取值范围);
(3)当点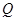 运动时,是否存在以
运动时,是否存在以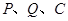 为顶点的三角形与△
为顶点的三角形与△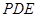 相似?若存在,求出
相似?若存在,求出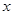 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
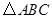 中,
中,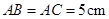 ,
,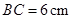 ,点
,点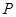 从点
从点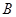 开始沿
开始沿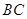 边以每秒1
边以每秒1 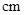 的速度向点
的速度向点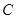 运动,点
运动,点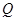 从点
从点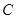 开始沿
开始沿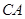 边以每秒2
边以每秒2 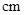 的速度向点
的速度向点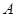 运动,
运动,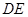 保持垂直平分
保持垂直平分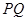 ,且交
,且交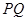 于点
于点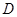 ,交
,交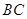 于点
于点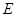 .点
.点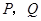 分别从
分别从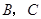 两点同时出发,当点
两点同时出发,当点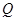 运动到点
运动到点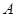 时,点
时,点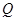 、
、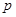 停止运动,设它们运动的时间为
停止运动,设它们运动的时间为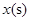 .
.(1)当
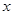 = 秒时,射线
= 秒时,射线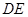 经过点
经过点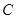 ;
;
(2)当点
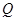 运动时,设四边形
运动时,设四边形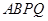 的面积为
的面积为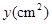 ,求
,求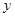 与
与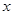 的函数关系式(不用写出自变量取值范围);
的函数关系式(不用写出自变量取值范围);(3)当点
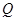 运动时,是否存在以
运动时,是否存在以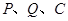 为顶点的三角形与△
为顶点的三角形与△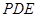 相似?若存在,求出
相似?若存在,求出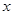 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.解:(1) ……………3分
……………3分
(当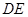 经过点
经过点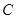 时,∵
时,∵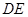 ⊥
⊥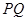 ,
,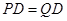 ∴
∴
 ,
,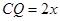
即 得
得
∴当 时,当
时,当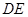 经过点
经过点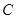 )
)
(2)分别过点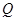 、
、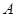 作
作 ,
,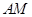 ⊥
⊥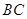 垂足为
垂足为 、
、 .
.
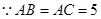 cm,
cm,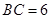 cm, ∴
cm, ∴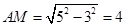 (cm)
(cm)
∵ ∴
∴
∴ 即
即
 ……………6分
……………6分
又 ∴
∴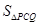 =
= =
=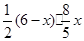
∴ =
= -
-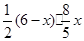
即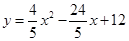 ……………9分
……………9分
(3)存在. ……………10分
理由如下:
∵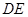 ⊥
⊥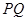 ∴
∴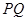 ⊥
⊥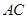 时△
时△ ∽△
∽△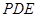
此时,△ ∽△
∽△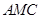
∴ 即
即  ∴
∴ ……………12分
……………12分
 ……………3分
……………3分(当
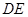 经过点
经过点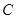 时,∵
时,∵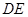 ⊥
⊥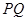 ,
,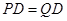 ∴
∴
 ,
,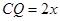
即
 得
得
∴当
 时,当
时,当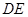 经过点
经过点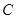 )
)(2)分别过点
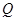 、
、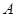 作
作 ,
,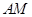 ⊥
⊥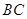 垂足为
垂足为 、
、 .
. 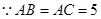 cm,
cm,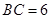 cm, ∴
cm, ∴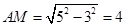 (cm)
(cm)∵
 ∴
∴
∴
 即
即
 ……………6分
……………6分又
 ∴
∴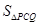 =
= =
=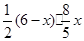
∴
 =
= -
-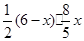
即
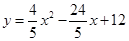 ……………9分
……………9分(3)存在. ……………10分
理由如下:
∵
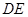 ⊥
⊥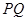 ∴
∴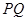 ⊥
⊥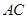 时△
时△ ∽△
∽△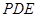
此时,△
 ∽△
∽△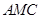
∴
 即
即  ∴
∴ ……………12分
……………12分(1)由于DE垂直平分PQ,所以只要CP=CQ,根据等腰三角形的性质,DE又是顶角的平分线,所以列出方程,求出x=2.
(2)由于四边形AQPB的形状不规则,所以可以用△ABC的面积减去△PQC的面积,而△PQC的面积可以用x表达,则四边形AQPB的面积也可以用x表达出来.
(3)假设存在,根据已知条件,易证△PQC∽△AMC,所以 ,
,
所以 ,即x=
,即x= 
解:(1)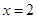 ……………3分
……………3分
(当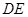 经过点
经过点 时,∵
时,∵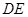 ⊥
⊥ ,
,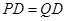 ∴
∴
 ,
,
即 得
得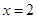
∴当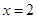 时,当
时,当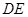 经过点
经过点 )
)
(2)分别过点 、
、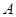 作
作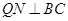 ,
,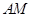 ⊥
⊥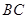 垂足为
垂足为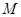 、
、 .
.
 cm,
cm, cm, ∴
cm, ∴ (cm)
(cm)
∵ ∴
∴
∴ 即
即
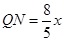 ……………6分
……………6分
又 ∴
∴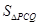 =
=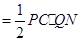 =
=
∴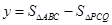 =
= -
-
即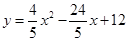 ……………9分
……………9分
(3)存在. ……………10分
理由如下:
∵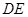 ⊥
⊥ ∴
∴ ⊥
⊥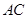 时△
时△ ∽△
∽△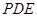
此时,△ ∽△
∽△
∴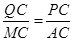 即
即  ∴
∴ ……………12分
……………12分
(2)由于四边形AQPB的形状不规则,所以可以用△ABC的面积减去△PQC的面积,而△PQC的面积可以用x表达,则四边形AQPB的面积也可以用x表达出来.
(3)假设存在,根据已知条件,易证△PQC∽△AMC,所以
 ,
,所以
 ,即x=
,即x= 
解:(1)
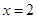 ……………3分
……………3分(当
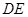 经过点
经过点 时,∵
时,∵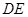 ⊥
⊥ ,
,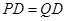 ∴
∴
 ,
,
即
 得
得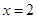
∴当
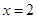 时,当
时,当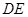 经过点
经过点 )
)(2)分别过点
 、
、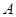 作
作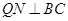 ,
,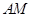 ⊥
⊥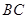 垂足为
垂足为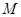 、
、 .
.  cm,
cm, cm, ∴
cm, ∴ (cm)
(cm)∵
 ∴
∴
∴
 即
即
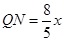 ……………6分
……………6分又
 ∴
∴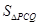 =
=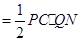 =
=
∴
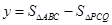 =
= -
-
即
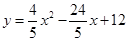 ……………9分
……………9分(3)存在. ……………10分
理由如下:
∵
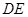 ⊥
⊥ ∴
∴ ⊥
⊥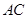 时△
时△ ∽△
∽△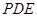
此时,△
 ∽△
∽△
∴
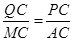 即
即  ∴
∴ ……………12分
……………12分
练习册系列答案
相关题目
 中,自变量
中,自变量 的取值范围是( )
的取值范围是( )


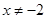

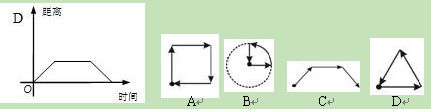
 中自变量x的取值范围是 .
中自变量x的取值范围是 . 中,自变量x的取值范围是
中,自变量x的取值范围是



 ,试研究该函数的性质.
,试研究该函数的性质. 的图象经过点A(1,-1),那么
的图象经过点A(1,-1),那么 ____,该函数图象与
____,该函数图象与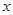 轴的交点坐标是_____,与
轴的交点坐标是_____,与 轴的交点坐标是_____
轴的交点坐标是_____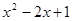 )可以由E(x,
)可以由E(x,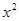 )怎样平移得到?
)怎样平移得到?