题目内容
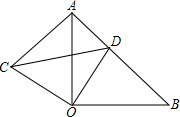 如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上.
如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上.(1)求证:△AOC≌△BOD;
(2)判断△CAD是什么形状的三角形,说明理由;
(3)若CD=2,AC=
| 3 |
分析:(1)根据题意得出∠1=∠2,进而利用SAS即可得出△AOC≌△BOD;
(2)利用△AOC≌△BOD,则∠CAO=∠DBO=45°,即可得出△CAD是直角三角形;
(3)利用∠ACD=30°,CD=2,结合直角三角形中30°所对的边等于斜边的一半得出AD=
CD=1,得出AB=AD+BD=AD+AC即可得出答案.
(2)利用△AOC≌△BOD,则∠CAO=∠DBO=45°,即可得出△CAD是直角三角形;
(3)利用∠ACD=30°,CD=2,结合直角三角形中30°所对的边等于斜边的一半得出AD=
| 1 |
| 2 |
解答: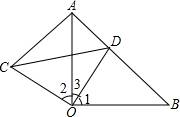 (1)证明:∵△AOB和△COD均为等腰直角三角形,
(1)证明:∵△AOB和△COD均为等腰直角三角形,
∠AOB=∠COD=90°,
∴∠1=90°-∠3,∠2=90°-∠3,
∴∠1=∠2,
在△AOC和△BOD中
,
∴△AOC≌△BOD(SAS);
(2)解:△CAD是直角三角形;
理由:∵△AOC≌△BOD,
∴∠CAO=∠DBO=45°,
又∠BAO=45°,
∴∠CAD=90°,
∴△CAD是直角三角形;
(3)解:在Rt△CAD中,∠ACD=30°,CD=2,
∴AD=
CD=1,
又∵△AOC≌△BOD,
∴AC=BD,
∴AB=AD+BD=AD+AC=1+
.
 (1)证明:∵△AOB和△COD均为等腰直角三角形,
(1)证明:∵△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,
∴∠1=90°-∠3,∠2=90°-∠3,
∴∠1=∠2,
在△AOC和△BOD中
|
∴△AOC≌△BOD(SAS);
(2)解:△CAD是直角三角形;
理由:∵△AOC≌△BOD,
∴∠CAO=∠DBO=45°,
又∠BAO=45°,
∴∠CAD=90°,
∴△CAD是直角三角形;
(3)解:在Rt△CAD中,∠ACD=30°,CD=2,
∴AD=
| 1 |
| 2 |
又∵△AOC≌△BOD,
∴AC=BD,
∴AB=AD+BD=AD+AC=1+
| 3 |
点评:此题主要考查了全等三角形的判定与性质以及直角三角形的判定方法,根据全等三角形的判定AOC≌△BOD是解题关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 15、如图,∠AOB和一条定长线段a,在∠AOB内找一点P,使P到OA,OB的距离都等于a,做法如下:
15、如图,∠AOB和一条定长线段a,在∠AOB内找一点P,使P到OA,OB的距离都等于a,做法如下: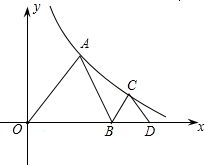 如图,△AOB和△BCD都是等边三角形,点A、C在函数
如图,△AOB和△BCD都是等边三角形,点A、C在函数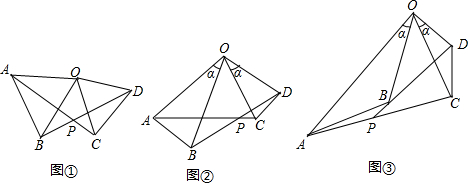
 如图,∠AOB和∠AOD分别是∠AOC的余角和补角,且OC是∠BOD的平分线,求∠AOC的度数.
如图,∠AOB和∠AOD分别是∠AOC的余角和补角,且OC是∠BOD的平分线,求∠AOC的度数.