题目内容
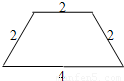
如图，这是一张等腰梯形纸片，它的上底AD长为2cm，下底BC长为4cm，腰长CD为2cm．求该梯形的高AE的长．
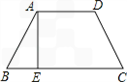
解：作DF⊥BC于F
∵四边形ABCD是等腰梯形，
∴AB=CD，∠B=∠C，AE=DF，
∴△ABE≌△DCF，
∴BE=CF=
（BC﹣AD）=2
在Rt△ABE中，根据勾股定理AE=
=
=
cm
答：该梯形的高AE的长为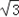
cm．
∵四边形ABCD是等腰梯形，
∴AB=CD，∠B=∠C，AE=DF，
∴△ABE≌△DCF，
∴BE=CF=
（BC﹣AD）=2 在Rt△ABE中，根据勾股定理AE=
==cm答：该梯形的高AE的长为
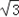cm．
练习册系列答案
相关题目
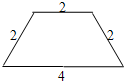33、如图，这是一张等腰梯形纸片，它的上底长为2，下底长为4，腰长为2，这样的纸片共有5张．打算用其中的几张来拼成较大的等腰梯形，那么你能拼出哪几种不同的等腰梯形？分别画出它们的示意图，并写出它们的周长．
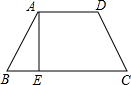如图，这是一张等腰梯形纸片，它的上底AD长为2cm，下底BC长为4cm，腰长CD为2cm．求该梯形的高AE的长．
