题目内容
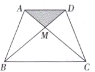
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,沿着
点出发,沿着![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 点运动;同时点
点运动;同时点![]() 从
从![]() 点出发,沿
点出发,沿![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 点运动,设运动时间为
点运动,设运动时间为![]() .
.
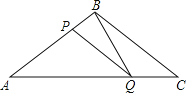
(1)当![]() 为何值时,
为何值时,![]() ;
;
(2)当![]() ,求
,求![]() 的值;
的值;
(3)![]() 能否与
能否与![]() 相似?若能,求出
相似?若能,求出![]() 的长;若不能,请说明理由.
的长;若不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)当PQ∥BC时,根据平行线分线段成比例定理,可得出关于AP,PQ,AB,AC的比例关系式,我们可根据P,Q的速度,用时间x表示出AP,AQ,然后根据得出的关系式求出x的值.
(2)我们先看当![]() =
=![]() 时能得出什么条件,由于这两个三角形在AC边上的高相等,那么他们的底边的比就应该是面积比,由此可得出CQ:AC=1:3,那么CQ=10cm,此时时间x正好是(1)的结果,那么此时PQ∥BC,由此可根据平行这个特殊条件,得出三角形APQ和ABC的面积比,然后再根据三角形PBQ的面积=三角形ABC的面积-三角形APQ的面积-三角形BQC的面积来得出三角形BPQ和三角形ABC的面积比.
时能得出什么条件,由于这两个三角形在AC边上的高相等,那么他们的底边的比就应该是面积比,由此可得出CQ:AC=1:3,那么CQ=10cm,此时时间x正好是(1)的结果,那么此时PQ∥BC,由此可根据平行这个特殊条件,得出三角形APQ和ABC的面积比,然后再根据三角形PBQ的面积=三角形ABC的面积-三角形APQ的面积-三角形BQC的面积来得出三角形BPQ和三角形ABC的面积比.
(3)本题要分两种情况进行讨论.已知了∠A和∠C对应相等,那么就要分成AP和CQ对应成比例以及AP和BC对应成比例两种情况来求x的值.
解:(1)由题意得,![]() 平行于
平行于![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)∵![]() ,
,
∴![]() ,
,![]() ,
,
∴时间用了![]() 秒,
秒,![]() ,
,
∵由(1)知,此时![]() 平行于
平行于![]() ,
,
∴![]() ,相似比为
,相似比为![]() ,
,
∴![]() .
.
∴四边形![]() 与三角形
与三角形![]() 面积比为
面积比为![]() ,即
,即![]() ,
,
又∵![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() .
.
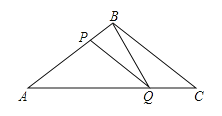
(3)假设两三角形可以相似.
情况1:当![]() 时,
时,![]() ,即有
,即有![]() 解得
解得![]() ,
,
经检验,![]() 是原分式方程的解.
是原分式方程的解.
此时![]() ,
,
情况2:当![]() 时,
时,![]() ,即有
,即有![]() 解得
解得![]() ,
,
经检验,![]() 是原分式方程的解.
是原分式方程的解.
此时![]() .
.
综上所述,![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】已知函数y=y1y2,其中y1=![]() +1,y2=
+1,y2=![]() x﹣1,请对该函数及其图象进行如下探究:
x﹣1,请对该函数及其图象进行如下探究:
解析式探究:根据给定的条件,可以确定出该函数的解析式为:______.
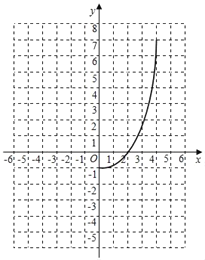
函数图象探究:①根据解析式,完成下表:
x | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | ﹣9 | ﹣ | m | n | ﹣1 | ﹣ | … |
m=______,n=_____.
②根据表中数据,在如图所示的平面直角坐标系中描点,并画出当x≤0时的函数图象;
结合画出的函数图象,解决问题:
①若A(x1,y1)、B(x2,y2)为图象上的两点,满足x1<x2;则y1_____y2(用<、=、>填空).
②写出关于x的方程y1y2=﹣x+3的近似解(精确到0.1).